 SCIENCES DE
L'INGENIEUR
SCIENCES DE
L'INGENIEUR
Niveau : Première générale, enseignement de spécialité SI
D
É
C
O
N
N
E
C
T
É
TD : Acquisition de l'information
Exercice 1 : Drone

L’AR drone de Parrot possède un capteur de distance permettant de contrôler l’altitude du drone.
Ses caractéristiques sont données par le tableau suivant :
| Tension d’alimentation | 3.2~5.2V |
|---|---|
| Courant de fonctionnement | 8mA |
| Fréquence ultrasonique | 40kHz |
| Plage de mesure | 2-350cm |
| résolution | 1cm |
| Type de sortie | Impulsion en ms |
| Taille du capteur | 50mm X 25mm X 16mm |
| Poids du capteur | 13g |
| Angle de mesure | 15 degrés |
| Température de fonctionnement | -10 à 60 °C |
Les simulations donnent les résultats suivants :
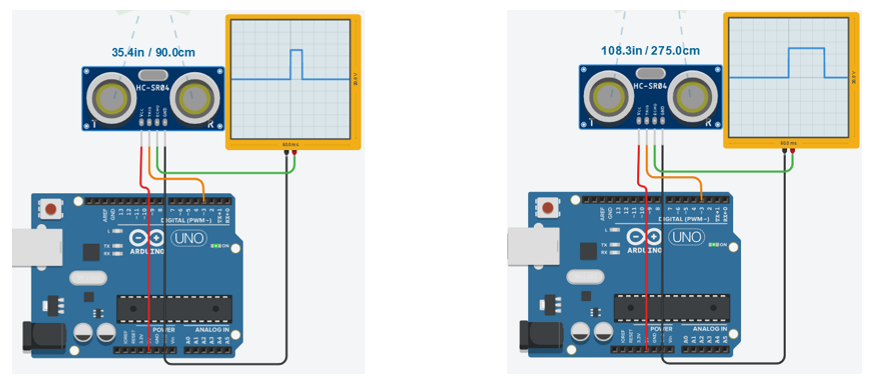
Les échèles sont les suivantes : 5ms/division pour les temps (axe X) et 2V/division pour la tension (axe Y)
Quelle est la tension d'alimentation du capteur ?
On donne la relation suivante permettant de calculer la distance en fonction de la durée de l’impulsion haute.
La durée de l’impulsion est en secondes et la vitesse du son en m.s-1
Compléter le tableau ci-dessous :
| Distance simulée (m) | durée de l'impusion (s) | distance calculée (m) | Erreur (m) |
|---|---|---|---|
| 0,90 | |||
| 2,75 |
Que peut-on dire sur le type d’erreur du capteur ?
Exercice 2 : Thermomètre
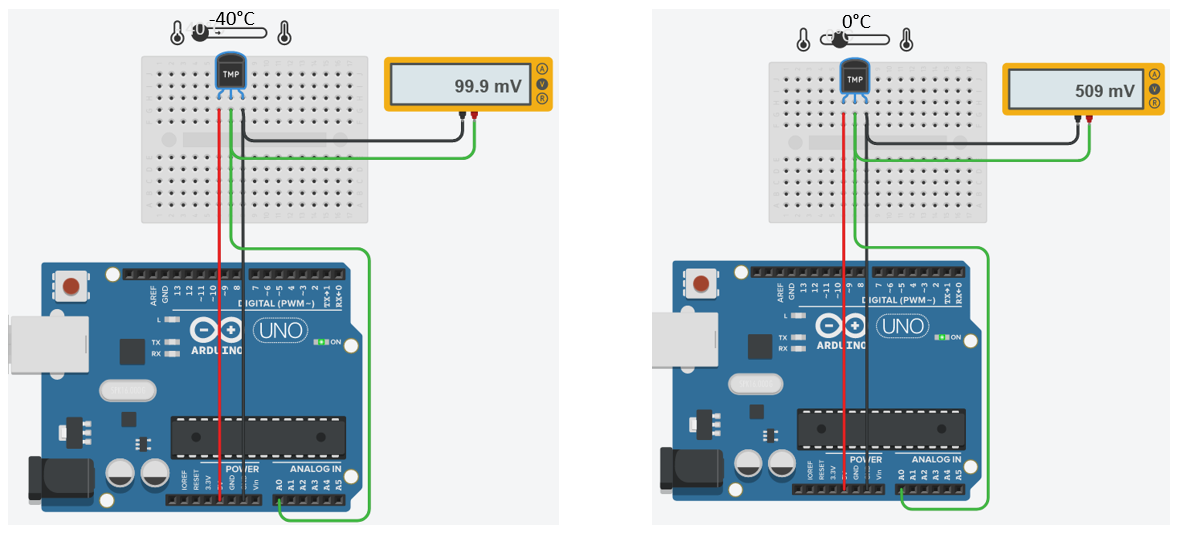
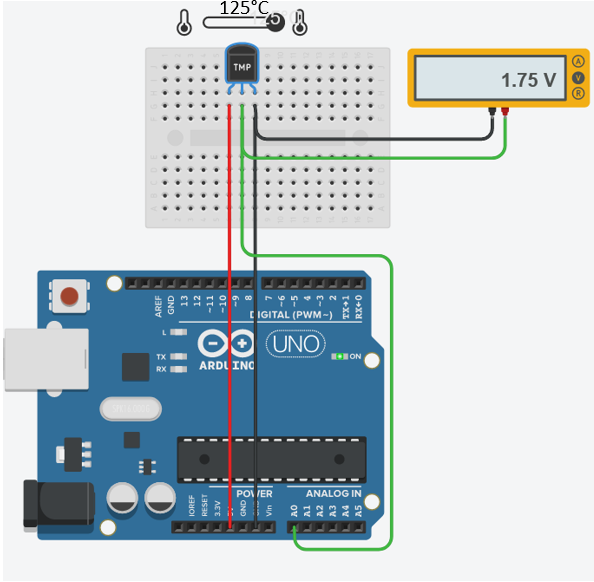
Complétez le tableau ci-dessous
| Température (°C) | Tension (V) |
|---|---|
Ce capteur fait partie de quelle famille ?
Montrez par calcul que le facteur d’échelle donné par le constructeur est de 10mV/°C
Le graphique ci dessous représente l'évolution de la tension en fonction de la température.
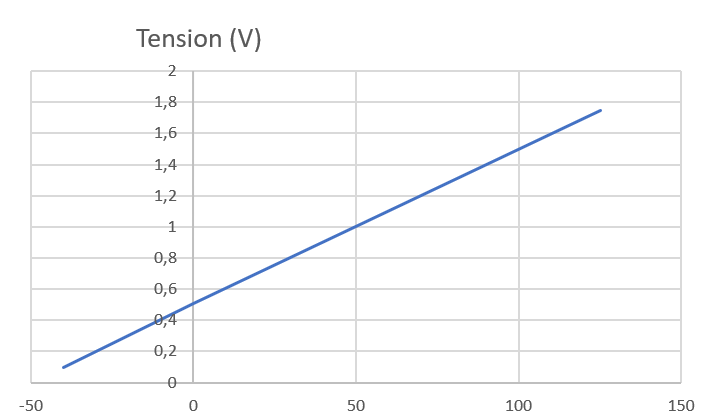
Relever graphiquement la valeur de la tension délivrée par le capteur lorsque la température est de 50°C
Le capteur est connecté à l’entrée analogique A0 du microcontrôleur Arduino. Celui-ci possède un convertisseur analogique numérique 10 bits. Sa tension de référence est de 5V.
Calculez le quantum, puis la sensibilité en °C. Cette méthode engendrera quel type d'erreur ?
Exercice 3 : Pesée de cartouche de gaz

Les cartouches de gaz CV360 sont utilisée dans les lampes à souder par exemple. Le système représenté ci-dessous permet de vérifier le poids des cartouches après remplissage de celles-ci. Pour cela un capteur de force transforme le poids en une tension U proportionnelle à celui-ci. Elle est ensuite convertie en un signal numérique B sur 7 bits (B0 à B6).
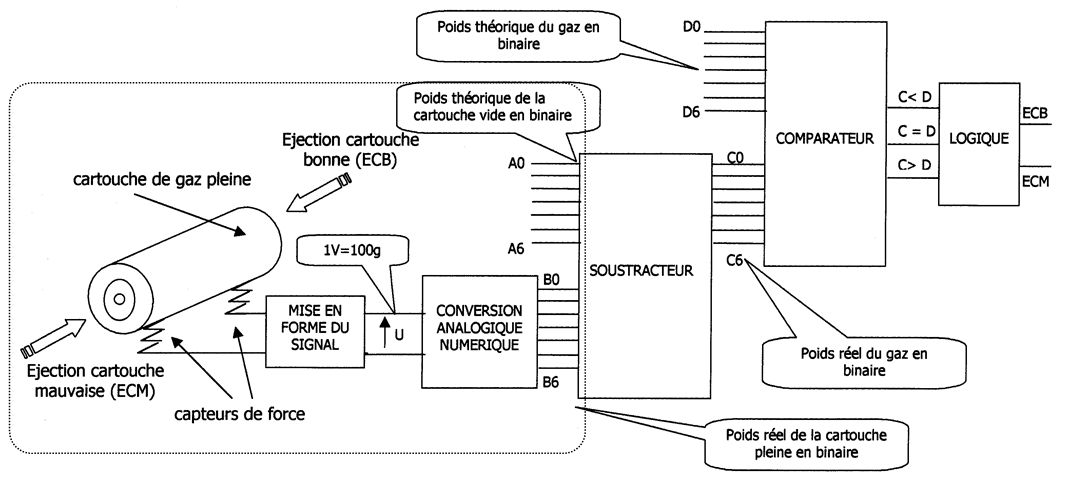
Mise en forme du signal :
Q1. D'après les caractéristiques du capteur de poids (1V pour 100g), calculer sa sensibilité en V/g
Convertisseur analogique numérique
Q2. D'après le nombre de bits utilisés par le convertisseur analogique numérique, calculer la résolution (le quantum) lorsque la tension Vref = 5V
Q3. Démontrez que la sensibilité du signal numérisé est de 3.9 grammes
Q4. Calculer le poids maximal mesurable, lorsque la tension U=5V
Soustracteur
On soustrait au chiffre binaire B, le chiffre binaire A qui représente le poids théorique de la cartouche vide et on obtient le chiffre binaire C qui représente le poids réel du gaz contenu dans la cartouche.
Le chiffre C est comparé au chiffre D qui représente le poids théorique minimum que devrait contenir une cartouche.
Si C est supérieur ou égal à D, ECB=1 et on commande un vérin qui évacue la cartouche conforme vers le système de conditionnement.
Si C est inférieur à D, ECM=1 et on commande un vérin qui évacue la cartouche non conforme vers un bac à rebuts.
Une cartouche vide pèse 62 grammes et le poids du gaz injecté est de 250 grammes.
Q5. Déterminer les codes binaires pour une cartouche vide puis pour le poids du gaz.
Comparateur et logique
Q6. Lors d'une mesure, le soustracteur indique un code binaire 0b 100 0010. La cartouche est-elle presque pleine, pleine ou trop remplie ? Faudra-t-il actionner ECB ou ECM ?
On voit que lorsque C=D alors ECM = 1
On donne les tables de vérité des fonctions logiques suivantes :
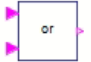
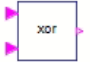
| Fonction OU | Fonction ET | Fonction XOR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | D | ECM | C | D | ECM | C | D | ECM | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | ||||
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | ||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | ||||
 |  |  | ||||||||||
Q7. Compléter la table de vérité ci-dessous
| C<D | C>D | ECM |
|---|---|---|
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 | 0/1 |
Remarque : La dernière ligne de la table de vérité est un état qui ne peut pas arriver car C ne peut pas être inférieur D et C ne peut pas être supérieur à D en même temps. On peut donc donner n'importe quel état à ECM (0 ou 1)
Q8. Indiquez les deux fonctions logiques qu'on peut choisir pour commander ECM
Q9. Compléter le schéma structurel du comparateur ci-dessous, en plaçant : C<D - C=D - C>D - ECB - ECM et l'une des fonctions trouvées précédemment
Exercice 4 : Robot anti-incendie


Le robot est contrôlé à distance par un opérateur à l’aide d’un pupitre de commande.
Il est constitué d’une turbine Magirus portée par un tracteur à chenilles.
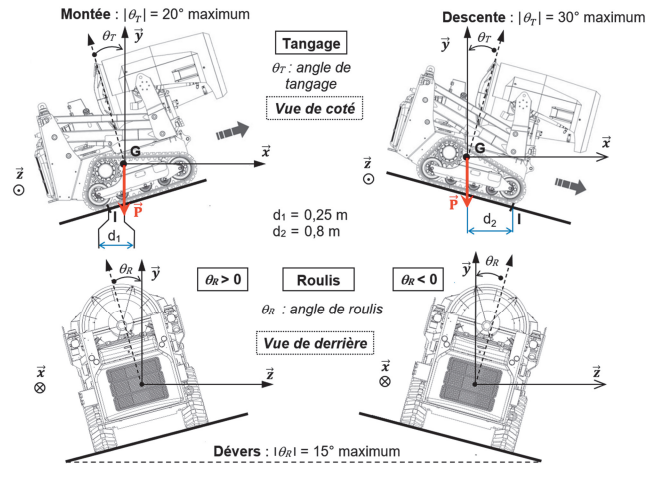
Lors de son déplacement sur une pente ou un devers, il faut contrôler son l'inclinaison afin d'éviter qu'il ne se renverse.
L'angle maximal en pente est limité à 20° en montée, 30° en descente et à 15° en dévers (voir figure ci-dessous)
La figure ci-dessous représente les deux axes de cet inclinomètre et la caractéristique obtenue pour la plage de mesure de -45° à +45° de chaque angle. Le signal obtenu est une tension US variant de 0 à 5 V, représentative de l’angle d’inclinaison.
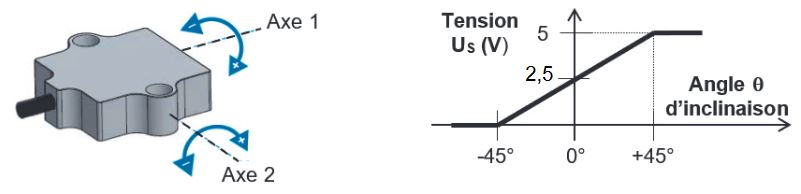
Q1. À partir de la caractéristique de l’inclinomètre, établir l’équation de la tension US en fonction de l’angle θ pour la plage de mesure [-45°,+45°] de cet inclinomètre.
Q2. A partir de l'équation précédente, calculer les tensions délivrées par le capteur pour les angles suivants
Un convertisseur analogique numérique CAN permet de numériser la tension US (tension variant de 0 à 5 V issue de l’inclinomètre) en un signal numérique N codé sur 10 bits, représentatif de l’angle de roulis θR ou l'angle de tangage θT selon l'axe.
Le diagramme de blocs internes [ibd] de la chaîne d’information est donné ci-dessous

Q3. Préciser la nature du flux d'information correspondant aux points A, B et C de la figure 5 (analogique ou numérique).
Q4. Après avoir calculé le quantum du CAN, compléter le tableau donnant les différentes valeurs de tension US et N issues de la numérisation (valeurs de N en décimal, puis en binaire).
| Angle | tension | Signal numérique N (sur 10 bits) | |
|---|---|---|---|
| Décimal | binaire | ||
| +45° | 1023 | ||
| +20° | |||
| +15° | |||
| 0° | |||
| -15° | |||
| -30° | |||
| -45° | |||
Q5. Montrer que la précision en degré issue de la numérisation de l’angle de roulis θR est inférieure à 0,1° conformément au cahier des charges.
Q6. Compléter l'algorithme suivant en remplaçant les ?, afin de faire retentir 2 alarmes sonores différentes (ALARME1 ou ALARME2) lorsque les angles maximums de roulis θR ou de tangage θT sont dépassés.
- NR représente la valeur convertie par le CAN de l'angle de roulis,
- NT représente la valeur convertie par le CAN de l'angle de tangage.
Pascal Hassenforder 19/01/2022
Mise à jour : 14/05/2023