La grandeur physique est la température dans la maison.

Un capteur traduit cette grandeur physique en un signal électrique proportionnel (information analogique).

Un convertisseur traduit l'information analogique en une information numérique (nombre binaire codé sur plusieurs fils). Cette information est traitée pour le calcul et l'affichage de la température.

L'utilisateur règle la température voulue. Cette consigne est comparée à la température mesurée pour produire un signal logique qui active ou stoppe le chauffage

2.1. POIDS FORT ET POIDS FAIBLE

Dans un nombre, le poids faible correspond au chiffre ayant l'influence la plus petite (c'est le chiffre le plus à droite).

Dans un nombre, le poids fort correspond au chiffre ayant l'influence la plus grande (c'est le chiffre le plus à gauche).

Exemple : dans le nombre décimal 4 589 237 : le chiffre de poids fort est : , le chiffre de poids faible est :

2.2. BASE D'UN NOMBRE

Dans l'étude des systèmes automatisés il est souvent nécessaire d'utiliser plusieurs bases de numérotation pour un même nombre. Les nombres sont convertis le plus souvent en trois bases.

2.3. BASE 10 : DECIMALE

C'est la manière de numéroter la plus courante, mais pas la plus pratique à utiliser en informatique.

Un nombre en base 10 est représenté sans préfixe. Ex 2356.

Il se décompose comme suit : 2xBase^Rang + 3xBase^Rang + 5xBase^Rang + 6xBase^Rang
Donc Base = 10 donc :            2x10³       +   3x10²       +   5x10¹       +   6x10⁰

2.4. BASE 2 : BINAIRE

Dans la base 2 tous les nombres sont uniquement formés par deux chiffres 0 et 1.

Les minuscules interrupteurs électroniques des microprocesseurs ne connaissent que deux états, ouvert ou fermé (0 ou 1). Le langage interne de tout système automatisé est donc basé sur le système binaire. Il existe plusieurs variétés de codes binaires, les plus utilisés seront étudiés dans cette leçon. Un nombre écrit en binaire naturel est représenté avec un préfixe 0b ou 0b. Ex 0b110011

Un nombre écrit en binaire BCD est représenté avec un préfixe (BCD). Ex (BCD)110011

2.5. BASE 16 : HEXADECIMALE

Dans la base 16 il faut 16 signes différents pour représenter un chiffre 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. les lettres A à F ont été utilisées pour compléter ce code.

Ce code est très pratique à utiliser en informatique

Un nombre écrit en hexadécimal est représenté avec un préfixe 0x ou $

Exemple : 0x1AC2BF ou $FF0000

REMARQUE : Il est très important de connaître les différents préfixes car les nombres 10110, 0b10110, 0x10110 et (BCD)10110 sont tous différents.

Une variable binaire est appelé BIT. Un bit peut prendre la valeur 0 ou 1

Un QUARTET est un nombre formé de 4 bit. (Il peut prendre 2^4 combinaisons soit 16 valeurs)

Un OCTET (BYTE) est un nombre formé de 8 bit. (Il peut prendre valeurs)

Un MOT (WORD) est un nombre formé de 16 bit. (Il peut prendre valeurs)

Un MOT LONG (DWORD) est un nombre formé de 32 bit. (Il peut prendre valeurs)

Longtemps l'informatique s'est singularisée par l'utilisation de différentes valeurs pour les unités du système international. Ainsi beaucoup d'informaticiens ont appris que 1 kilooctet valait 1024 octets. Or, depuis décembre 1998, l'organisme international IEC a statué sur la question. Voici donc les unités standardisées :

• Un kilooctet (ko ou kB) = 1000 octets
• Un Mégaoctet (Mo ou MB) = 1000 ko = 1 000 000 octets
• Un Gigaoctet (Go ou GB) = 1000 Mo = 1 000 000 000 octets
• Un Téraoctet (To) = 1000 Go = 1 000 000 000 000 octets

Attention ! De nombreux logiciels (parfois même certains systèmes d'exploitation) utilisent toujours la notation antérieure à 1998 pour laquelle :

• Un kilooctet (ko) = 210 octets = 1024 octets
• Un Mégaoctet (Mo) = 220 octets = 1024 ko = 1 048 576 octets …

L'IEC a également défini le kilo binaire (kibi), le méga binaire (Mébi), le giga binaire (Gibi), le tera binaire (Tebi).

Voici leurs définitions :

• Un kibioctet (kio ou kiB) vaut 2^10 = 1024 octets
• Un Mébioctet (Mio ou MiB) vaut 2^20 = 1 048 576 octets
• Un Gibioctet (Gio ou GiB) vaut 2^30 = 1 073 741 824 octets
• Un Tébioctet (Tio ou TiB) vaut 2^40 = 1 099 511 627 776 octets

C'est la base 2 qui n'utilise que 2 symboles : 0 et 1. Il est utilisé pour le calcul par les microprocesseurs

CODE BINAIRE NATUREL				CODE Décimal
d	c	b	a
0	0	0	0	0
0	0	0	1	1
0	0	1	0	2
0	0	1	1	3
0	1	0	0	4
0	1	0	1	5
0	1	1	0	6
0	1	1	1	7
1	0	0	0	8
1	0	0	1	9
1	0	1	0	10
1	0	1	1	11
1	1	0	0	12
1	1	0	1	13
1	1	1	0	14
1	1	1	1	15

4.1. PASSAGE DU CODE BINAIRE NATUREL AU CODE DECIMAL

Il faut utiliser les puissances de deux.

poids	28	27	26	25	24	23	22	21	20
	256	128	64	32	16	8	4	2	1
0b	1	1	0	0	0	0	1	0	1

0b110000101 = 1x256 + 1x128 + 0x64 + 0x32 + 0x16 + 0x8 + 1x4 + 0x2 + 1x1 =

Décodez l'heure donnée par la montre binaire :

4.2. PASSAGE DU CODE DECIMAL AU CODE BINAIRE NATUREL :

Une méthode de transcodage consiste à réaliser par des divisions par 2 successives

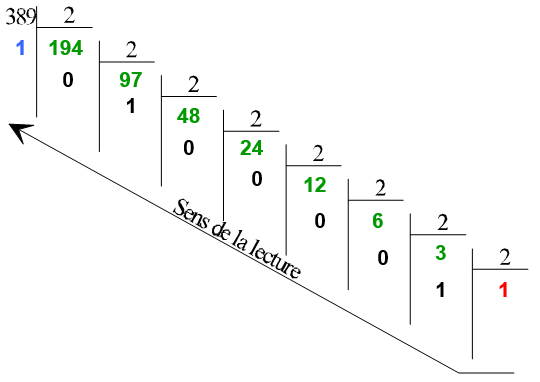
389 = 0b

Une seconde méthode consiste à remplir le tableau binaire à partir de la gauche. Tant que l'addition des poids reste inférieure ou égale au nombre décimal à convertir on place un 1 sinon 0:

	128	64	32	16	8	4	2	1
67	?	?	?	?	?	?	?	?

C'est le code utilisé dans l'électronique digitale. Il est constitué par une juxtaposition du code binaire limité à 9 (0b1001)

CODE BINAIRE NATUREL				CODE Décimal
d	c	b	a
0	0	0	0	0
0	0	0	1	1
0	0	1	0	2
0	0	1	1	3
0	1	0	0	4
0	1	0	1	5
0	1	1	0	6
0	1	1	1	7
1	0	0	0	8
1	0	0	1	9

5.1. PASSAGE DU CODE DECIMAL AU CODE BCD

Chaque chiffre décimal est codé individuellement en son équivalent en binaire naturel sur 4 bits

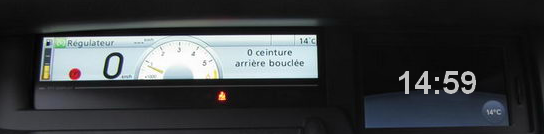
Exemple du codage de l'heure :"

Décimal	1	4	:	5	9
BCD

5.2. PASSAGE DU CODE BCD AU CODE DECIMAL

La méthode de transcodage est la même que précédemment, mais dans le sens inverse. On groupe le code BCD par quartets (à partir de la droite), puis on converti chaque quartet en un chiffre décimal.

(BCD)1000 0110 1001 =

(BCD)11 1001 0110 =

Le code binaire est si éloigné de la pensée humaine que les informaticiens ont dû imaginer un moyen plus simple pour représenter des nombres binaires.

En effet dans les microprocesseurs toutes les informations sont codées en binaire. Les langages qui permettent de programmer ces microprocesseurs sont appelés. Il est impensable de programmer en binaire naturel.

Le code hexadécimal est un moyen de compacter le code en binaire naturel afin que l'écriture des programmes soit plus lisible.

Exemple du codage des couleurs

CODE BINAIRE NATUREL				CODE Hexadécimal
d	c	b	a
0	0	0	0	0
0	0	0	1	1
0	0	1	0	2
0	0	1	1	3
0	1	0	0	4
0	1	0	1	5
0	1	1	0	6
0	1	1	1	7
1	0	0	0	8
1	0	0	1	9
1	0	1	0	A
1	0	1	1	B
1	1	0	0	C
1	1	0	1	D
1	1	1	0	E
1	1	1	1	F

6.1 PASSAGE DE L'HEXADECIMAL AU CODE BINAIRE

Chaque chiffre décimal est codé individuellement en son équivalent en binaire naturel sur 4 bits

Hexa 0x	4	C	8	F
Binaire

0x4C8F = 0b

6.2. PASSAGE DU CODE BINAIRE NATUREL A L'HEXADECIMAL

La méthode de transcodage est la même que précédemment mais dans le sens contraire. On groupe le code binaire naturel par quartets (à partir de la droite) et on converti chaque quartet en un chiffre hexadécimal.

0b1100 0110 1100 = 0x

0b11 1001 1110 = 0x

6.3. PASSAGE DU CODE DECIMAL AU CODE HEXADECIMAL

Le transcodage se réalise par des divisions successives par 16

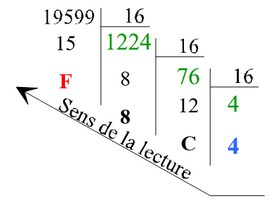
19599 = 0x

6.4. PASSAGE DU CODE HEXADECIMAL AU CODE DECIMAL

Il faut utiliser les puissances de 16

0x4C8F = x 16³ + x 16² + x 16¹ + x 16⁰

0x4C8F =

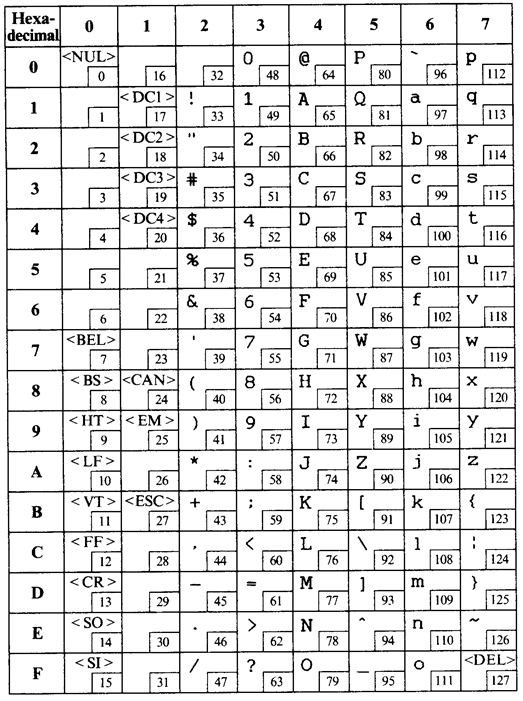
En informatique il est nécessaire d'utiliser des caractères (pour un texte).
Il est donc impératif d'utiliser un code convertissant les caractères en binaire naturel (ou hexadécimal).
Le code utilisé est le code ASCII (American Standard Code for Information Interchange).

Avant d'être utilisé en informatique ce code était utilisé pour la communication de messages à distance (TELEX). C'est pour cela qu'il comporte des caractères non imprimables (de 0x0 à 0x1F).
Ces codes non imprimables sont des protocoles de mise en page.

Exemple:

• 0x7 correspond à un "bip" sonore ()
• 0xD correspond au retour chariot
• 0xA correspond au passage à la ligne suivante

Un code ASCII est codé sur 1 octet

Rechercher le caractère de :

• (ASCII) 0x35 =
• (ASCII) 0x52 =
• (ASCII) 35 =