 SCIENCES DE L'INGENIEUR
SCIENCES DE L'INGENIEUR
Niveau : Terminale générale, enseignement de spécialité SI
D
É
C
O
N
N
E
C
T
É
TD : MICROCENTRALE VLH

L’implantation des turbines VLH permet un fonctionnement toute l’année en adaptant le débit de production (ouverture des pales) à celui de la rivière. La loi sur la pêche impose un débit réservé minimal pour la rivière de 10 % du débit annuel moyen, qui se traduit par une hauteur minimale de lame d’eau au niveau du barrage de 10 cm. L’ouverture des pales est asservie à la hauteur de la lame d’eau de façon à maintenir cette dernière à une hauteur supérieure à 10 cm. L’objet de cette étude est de faire une analyse des divers éléments entrant dans cette chaîne de régulation.

1 - OBJECTIF DE L’ÉTUDE
Les différentes parties proposées doivent permettre d’évaluer le gain énergétique de ces nouvelles centrales et de valider les solutions retenues pour répondre à la problématique environnementale : Comment maintenir un débit minimal sur une rivière équipée d’un parc de turbines totalement immergées ? Les données hydrométriques de la Mayenne dans le secteur d’implantation des VLH sont rapportées ci-dessous :
écoulements mensuels (naturels) - données calculées sur 41 ans
| janv. | févr. | mars | avril | mai | juin | juil. | août | sept. | oct. | nov. | déc. | Débit annuel moyen | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| débit (m3s-1) | 64,30 | 61,60 | 50,30 | 33,80 | 22,80 | 14,10 | 9,060 | 6,040 | 6,380 | 12,50 | 27,60 | 47,50 | 29,50 |

2 - GESTION DE L’OUVERTURE DES PALES
La turbine VLH autorise un fonctionnement à puissance réduite lorsque le débit de la rivière est inférieur au débit nominal de la turbine. Dans cette situation l’angle d’ouverture des pales est asservi à la hauteur de la lame d’eau. Un algorithme de commande élabore la consigne d’ouverture des pales en fonction de la hauteur de la lame d’eau, comme illustré par la figure ci-dessous :
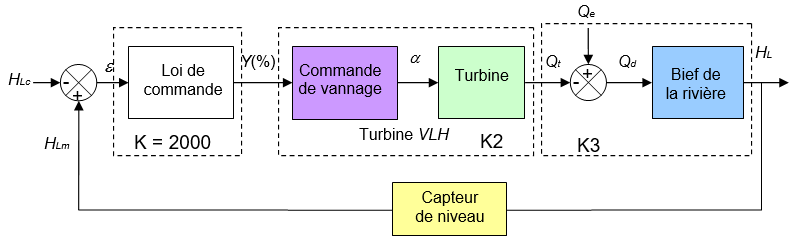
- HLc : consigne de hauteur de lame d’eau ;
- HLm : hauteur de lame d’eau mesurée ;
- HL : hauteur de lame d’eau réelle ;
- ε : écart entre la consigne et la mesure ;
- Y(%) : consigne de vannage (0 %, complètement fermé ; 100 %, complètement ouvert) ;
- a : angle d’ouverture des pales (0°, complètement fermé ; 24°, complètement ouvert) ;
- Qt : débit turbiné par la VLH ;
- Qe : débit d’entrée en amont du bief ;
- Qd : débit de débordement.
Compte tenu de l’étude sur le capteur de niveau, on considère que HLm = HL
3 - MODÉLISATION DU BIEF DE LA RIVIÈRE

L'objectif de cette partie est de trouver un modèle mathématique, d’un point de vue statique, du comportement de la rivière vis-à-vis du débit turbiné Qt par la VLH. La hauteur de la lame d’eau au droit du barrage est liée au débit de débordement Qd et peut être approchée par la relation suivante :
- Qd : débit de débordement en m3/s ;
- μ : constante estimée à 0,4 ;
- L : longueur utile de déversement du barrage ;
- g : constante d’accélération de la pesanteur 9,81 m/s2 ;
- HL : hauteur de débordement en m.
avec
On donne ci-dessous une vue aérienne d’un site d’implantation d’une des VLH

Q1 : le cahier des charges impose un débit réservé Qd supérieur à 10 % du débit annuel moyen. En vous référant aux données hydrométriques de la Mayenne, calculer la hauteur de lame d’eau HL en utilisant la relation suivante :
Q2 : L’automatisme de régulation de débit ayant une consigne de hauteur de lame d’eau de 10 cm, les exigences du cahier des charges seront-elles respectées en ce qui concerne le débit minimum de débordement (HL) ?
Q3 : D’après la vue aérienne ci-dessus, donner la relation liant Qe, Qd et Qt.
Q4 : Les turbines installées sont du type VLH 3550 (document technique DT2) et la hauteur de chute nette est de 2 m. Relever le débit Qt de la turbine.
débit : Qt = m3.s-1
Q5 : En vous référant aux données hydrométriques de la Mayenne estimer les mois de l’année durant lesquels il sera nécessaire de réguler le débit de la turbine pour satisfaire aux exigences du débit réservé Qd (HL=10cm).
calculs
réponse :
Q6 : La caractéristique HL = f(Qt) a l’allure donnée ci-dessous. Linéariser cette caractéristique autour de HL = 10 cm. Déterminer graphiquement sa fonction de transfert en calculant le coefficient directeur de cette droite :
Calcul du coefficient directeur :
4 - MODÉLISATION DE LA TURBINE
La commande de vannage (partie de système non étudié) permet d’obtenir une ouverture des pales plus ou moins grande en fonction d’une consigne de vannage Y(%) variant de 0 à 100 %. On considère que l’angle d’ouverture des pales a suit une loi linéaire en fonction de Y(%). Une illustration est donnée ci-dessous pour trois valeurs différentes de Y(%) :
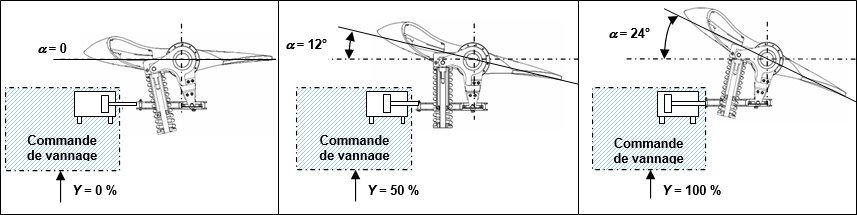
Q7 : tracer, sur le graphique suivant, la caractéristique de la commande de vannage a(°)=f(Y(%)). En considérant que le débit est proportionnel à l’angle a, que la hauteur de chute nette est de 2 m et que la turbine installée est une VLH 3550, tracer la caractéristique Qt(m3/s) = f(Y(%)), puis calculer K2.
Calcul de K2 :
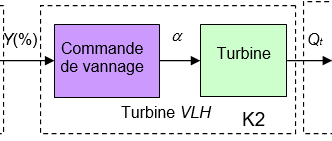
$K2=?/?$
5 - ÉTUDE DE LA LOI DE COMMANDE
La loi de commande est une loi dite à correction proportionnelle, c’est-à-dire sous la forme Y(%)= Kε où K représente le gain de l’action proportionnelle. Le but de l’étude qui suit est de déterminer la valeur du gain afin d’obtenir une précision (erreur statique) de 1 cm sur la hauteur de la lame d’eau.
Q8. Tracer, sur le le graphique suivant, la caractéristique de la loi de commande Y(%)=f(ε) où ε représente l’écart de hauteur de lame d’eau en mètre pour un gain K=2000. On rappelle que Y(%) ne peut pas être inférieure à 0 (turbine complètement fermée) et ne peut pas être supérieure à 100 (turbine complètement ouverte).
Préciser la zone, que l’on nommera BP (Bande proportionnelle), où la commande est effectivement proportionnelle à l’écart.
Sachant que ε = HL – HLc, représenter sur le graphique suivant, la caractéristique de la loi de commande Y(%) = f(HL) pour HLc=10 cm.
Préciser la zone, que l’on nommera BP (Bande proportionnelle), où la commande est effectivement proportionnelle à l’écart.
Q9. Pour une consigne HLc = 0.1 m, calculer HL avec K=2000, K2=0.125 et K3 = -0.018
Q10. Calculer l’erreur statique
En généralisant la transmittance de la chaîne directe est :
Kd = K x K2 x K3 HL = Kd x ε donc HL = Kd (HLC-HL) comme K4=1
d'ou :
Q11. Calculer la nouvelle valeur de K si on désire une hauteur de lame HL=11cm (HLC=0.1m)
Q12. Quelle influence a le gain K sur le débit réservé ? Que peut-il se passer si K est trop important ? Quel type de correcteur permettrait d'annuler l'erreur statique ?