 SCIENCES DE L'INGENIEUR
SCIENCES DE L'INGENIEUR
Niveau : Terminale générale, enseignement de spécialité SI
D
É
C
O
N
N
E
C
T
É
TP : TRANSAT BERCEUR

1. Introduction
Extrait du magazine © Enfant Magazine (article rédigé par Marie Auffret-Pericone avec le Dr Françoise Delormas, médecin) : « Aujourd’hui, pour calmer le nouveau-né, on redécouvre ce geste tendre, simple et ancestral du bercement »
Ces mouvements rythmés semblent avoir un effet bénéfique parce qu’ils recréent en partie les sensations qu’il a connues lorsqu’il était dans votre ventre.
Bercer bébé est un geste inné :
le bon rythme ? Celui-de votre cœur. Des études ont mis en évidence que le bercement le plus efficace comprend entre 60 et 70 oscillations par minute (proche des battements du cœur au repos), de faible amplitude ; votre bébé a ses préférences. Ce qu'il préfère ? Etre bercé d’avant en arrière, plutôt que de gauche à droite. Votre rythme doit être doux, répétitif et régulier. Vous constaterez que vous ralentissez progressivement l’allure quand vous allez et venez en berçant votre tout-petit dans vos bras ».
2. Présentation et caractéristiques du système étudié
Un moteur permet de mouvoir le transat horizontalement et l’autre verticalement. La régulation de la vitesse horizontale et l’asservissement de position du moteur vertical permettent de créer 5 mouvements de bercements différents et 6 vitesses de bercements : 10, 20, 30, 40, 50 et 60 bercements/min (ou tr/min ±10%)
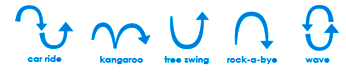
D'après la video, bercement naturel, quel mouvement de bercement est pratiqué ?
En relevant les points de la trajectoire du bébé sur la vidéo on obtient les signaux suivants :
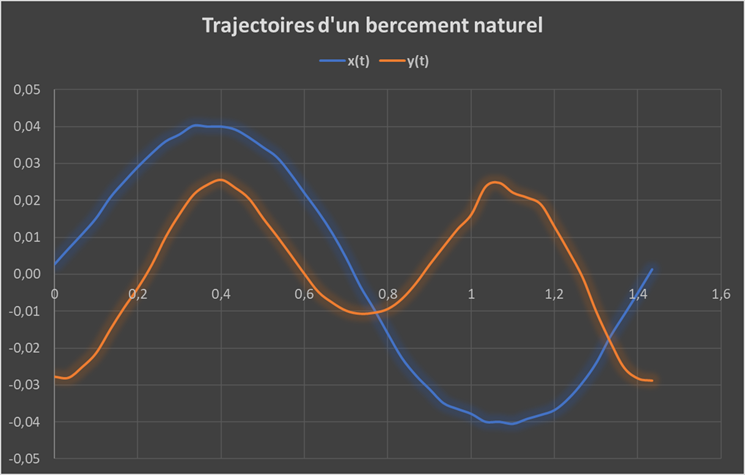
Les signaux s’apparentent à des sinusoïdes.
Déterminer l’amplitude A, la période T et le déphasage φ de chaque courbe :

Le calcul du déphasage se fait par un produit en croix : T -> 360°, t φ -> φ (°).
φ est positif s'il est en avance (figure ci-dessus) sinon φ est négatif s'il est en retard.
| x(t) | y(t) | |
|---|---|---|
| A(m) | ||
| T(s) | ||
| F(Hz) | ||
| φ(°) |
3. Modélisation mathématique du bercement
Description du modèle
Les courbes de déplacement horizontal x(t) et vertical y(t) déterminées à partir d’un bercement naturel sont similaires aux fonctions mathématiques sinusoïdales :
$x(t)=A*sin(omega*t)$ et $y(t)=B*sin(omega*t+phi)$
- A, B : Amplitude du signal en volts (V),
- $omega = 2*pi*f$: pulsation en rd/*s,
- $f = 1/t$ : fréquence en Hz,
- T : période en s,
- t : temps en s,
- $phi$: déphasage en rd.
Ouvrir le fichier sinusoides.xlsx et déterminer le nombre bercements/min, l’amplitude et le déphasage pour obtenir les résultats ci-dessous pour x(t) et y(t).
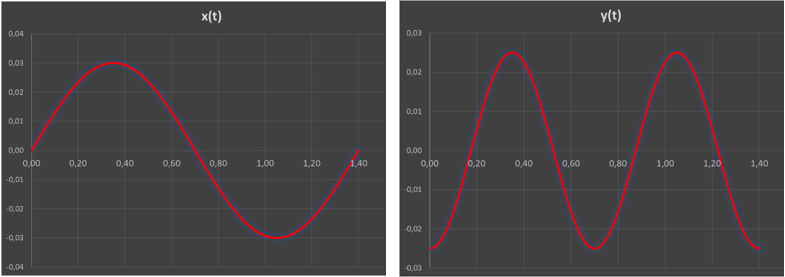
| x(t) | y(t) | |
|---|---|---|
| f(Hz) | ||
| Amplitude | ||
| Déphasage en ° | ||
| période (s) | ||
| Rapport Tx/Ty | ||
Ouvrir le fichier Excel « Trajectoires possibles.xlsx »
Remplir le tableau ci-dessous afin de trouver les mouvements de bercement possibles.

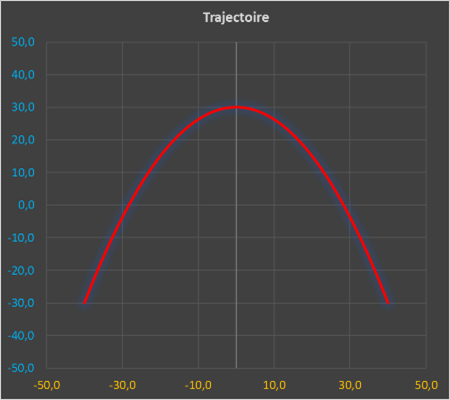
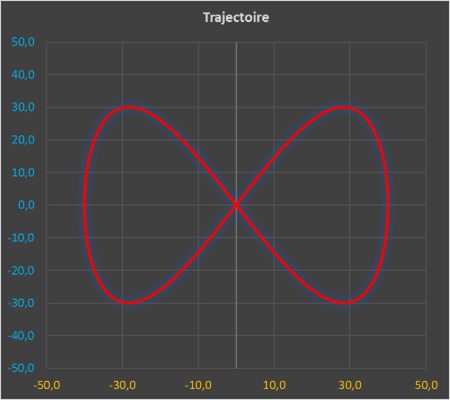

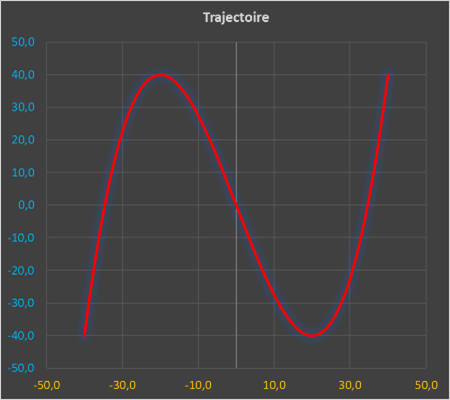
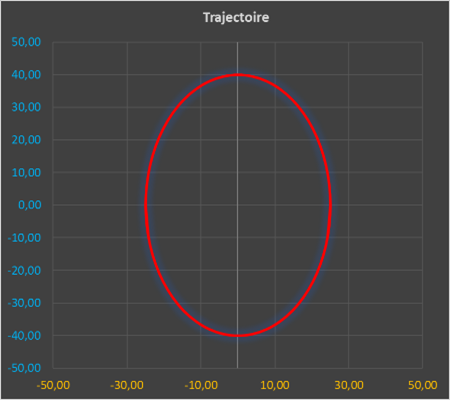
4. Modèle multiphysique du berceur :
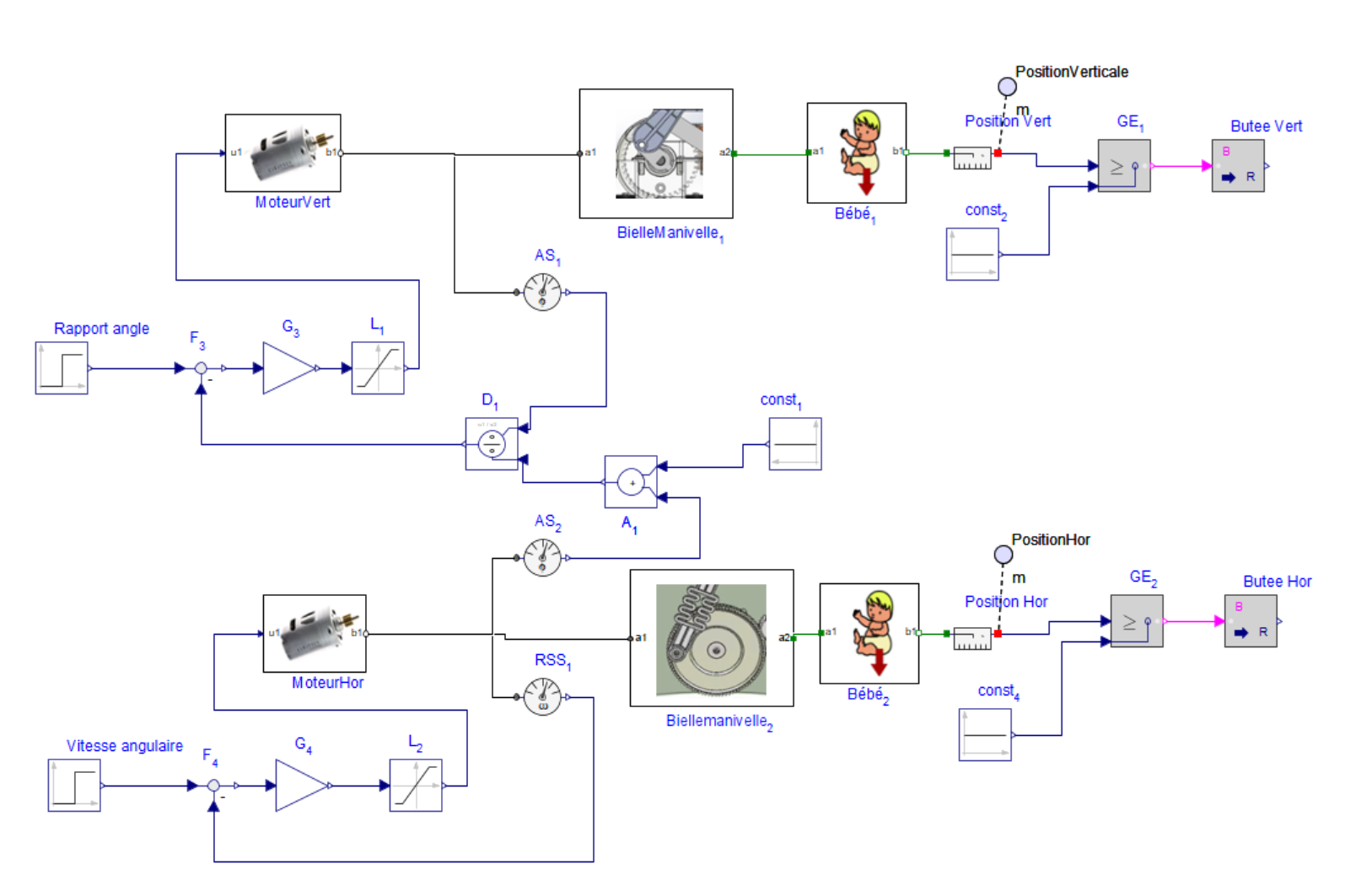
Exécuter le programme Maplesim puis charger le fichier « berceur.msim ». développer l’arbre et faire un double clic sur le schéma de la modélisation 
Cliquer sur le fond blanc du modèle pour voir ses paramètres :
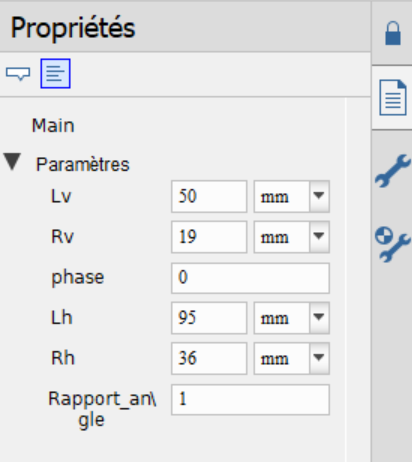
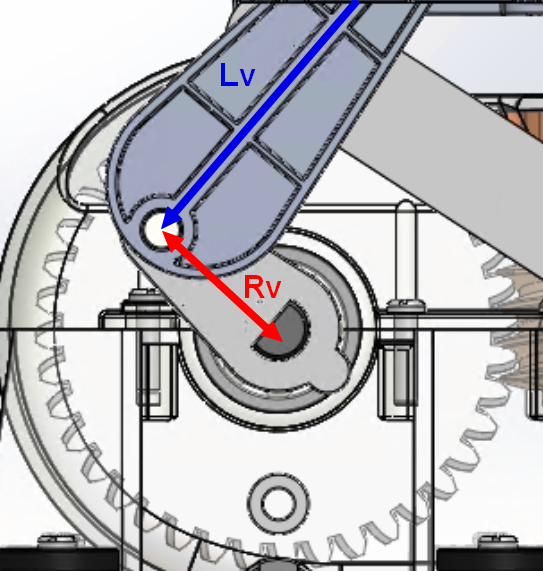
Lv représente la longueur de la manivelle et Rv le rayon de l'excentrique de la bielle-manivelle du système vertical
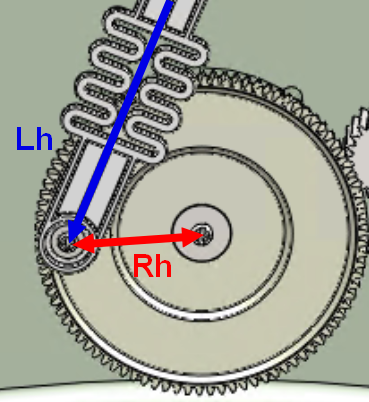
Lh représente la longueur de la manivelle et Rh le rayon de l'excentrique de la bielle-manivelle du système horizontal
Modifier le rapport d’angle et la phase du mouvement vertical afin de vérifier les 3 premières trajectoires.
Régler le temps de fin de simulation à 2.5 secondes puis lancer la simulation.
Effectuer les 3 simulations du tableau ci-dessous, cliquer sur le bouton droit de la souris sur la courbe simuléepour les enregistrer au format PNG.
Téléverser les courbes dans le tableau ci-dessous.
| Car ride | Wave | Tree swing |
|---|---|---|
Calcul des écarts entre l'attendu et la simulation
Relever les déplacements horizontaux et verticaux souhaités dans le diagramme des exigences. D'après les courbes de simulation, relever les amplitudes des déplacements horizontaux et verticaux simulé, puis calculer les écarts relatifs entre les déplacements attendus et les déplacements simulés.
Calcul des écarts entre l'attendu et la mesure
Mettre le berceur en mode wave avec la vitesse la plus basse.
A l'aide du pointeur laser implanté sur le berceur, tracer la courbe de déplacement puis mesurer l'amplitude du déplacement horizontal et vertical
Calculer les écarts relatifs entre les déplacements attendus et les déplacements mesurés.
5. Etude de la régulation de vitesse du berceur
Schéma blocs de la régulation de vitesse du moteur horizontal x(t)
Q1. Placez les éléments suivants : Motoréducteur, Capteur, Consigne, Hacheur, Correcteur.
Les vitesses angulaires attendues du moteur sur le déplacement horizontal correspondent aux 5
réglages permis par le bouton de sélection de la vitesse du berceur :
Vitesse N° Vitesse angulaire
en rad/s 1 1.1 2 1.4 3 1.7 4 2.1 5 2.6
Réponse à un échelon
Placer une sonde pour visualiser la consigne et une autre pour visualiser la vitesse angulaire.
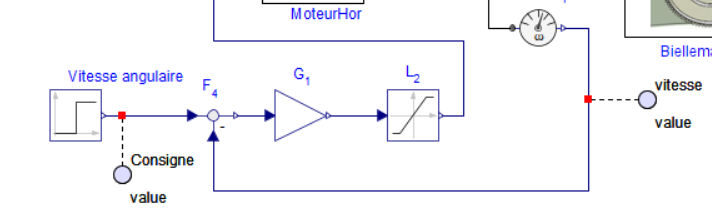
Imposer au modèle multiphysique la valeur de la consigne permettant de simuler la vitesse 3.
Lancer la simulation sur une durée de 1 seconde.
Dans la fenêtre des variables faire un double clic sur la valeur de la consigne pour afficher la courbe.
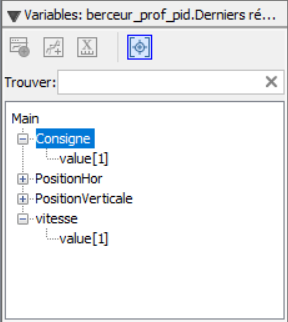
Développer la variable vitesse et glisser déposer-la sur le graphique précédent afin de voir les deux courbes sur le même graphe.
Relever et reporter ci-dessous les valeurs des graduations.



Compléter les graduations de l'axe des ordonnées
Relever sur le graphique ci-dessus
- Consigne :
- valeur finale :
- erreur statique :
Es=
- temps de réponse à ±5% :
Calcul des limites haute et basse :
Quel est l’ordre de l’asservissement ?
Paramétrage du correcteur proportionnel :
Le gain proportionnel K = 10, mais l’alimentation du moteur ne peut pas dépasser 12 volts
et ne peut pas descendre sous 0 volts, d’où le modèle suivant :

Ajuster le gain proportionnel k à 100 et lancer la simulation.
Faire une nouvelle simulation, insérez une sauvegarde de la courbe obtenue.
Quelle est l’influence de l’augmentation du gain proportionnel K1 ? quels sont les risques si K1 devient trop grand ?
Calcul des écarts entre l'attendu et la simulation
Calculer l'écart relatif entre la vitesse angulaire attendue et le simulé.
Correcteur PID
Remplacer le bloc du gain proportionnel par un bloc PID que vous trouverez dans "signal bloc" - "Controlers".
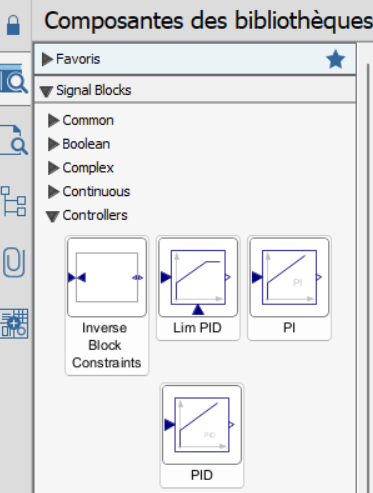
Configurer les paramètres du PID comme suit et faire les simulations sur 10s:
Téléverser les courbes dans le tableau ci-dessous.
k=2 Ti=0.5s Td=0.1s k=10 Ti=0.05s Td=0.1s k=50 Ti=1s Td=0.2s
Calcul des écarts entre l'attendu et la simulation

Calcul des écarts entre l'attendu et la mesure
Mesure de la vitesse angulaire du déplacement horizontal :
A chaque fois que le moteur effectue un tour, un capteur de fin de course s'active et passe à 5V.
Régler le berceur sur la vitesse 3.
Brancher l'oscilloscope sur le capteur de fin de course de l'interface ci-dessous et régler la base de temps de l'oscilloscope et
la sensibilité de la tension afin de visualiser le signal sur une période au moins.
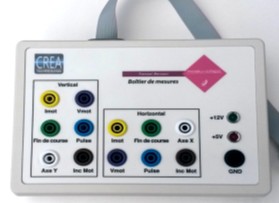
Déplacer les curseurs de mesure de l'oscilloscope afin de mesurer la période du signal.
Prendre une photo de l'oscillogramme de votre mesure.
Calculer la vitesse angulaire mesurée et les écarts relatifs entre l'attendu et le mesuré.
6. Etude de l’asservissement de position
Pour obtenir un bercement de type « tree swing », la vitesse de rotation du moteur vertical doit être deux fois plus grande
que la vitesse de rotation du moteur horizontal.
La consigne du rapport d’angle entre les deux moteurs doit donc être réglée à $(phi v)/(phi h)=2$.

Déterminer l’équation de R en fonction de φv, φh et K du modèle ci-dessus. En déduire le rôle de K=0,000001.
La simulation ci-dessous représente l’évolution de l’angle en rad des deux moteurs en fonction du temps.

D’après le graphique ci-dessus, justifiez que l’asservissement de position fonctionne bien.
Trouver un protocole de mesure permettant de vérifier que la vitesse angulaire verticale $omegav$ est 2 fois plus grande que la vitesse angulaire horizontale $omegah$. Consigner vos mesures.
Schéma blocs de la régulation de vitesse du moteur horizontal x(t)
Q1. Placez les éléments suivants : Motoréducteur, Capteur, Consigne, Hacheur, Correcteur.
Les vitesses angulaires attendues du moteur sur le déplacement horizontal correspondent aux 5 réglages permis par le bouton de sélection de la vitesse du berceur :
| Vitesse N° | Vitesse angulaire en rad/s |
|---|---|
| 1 | 1.1 |
| 2 | 1.4 |
| 3 | 1.7 |
| 4 | 2.1 |
| 5 | 2.6 |
Réponse à un échelon
Placer une sonde pour visualiser la consigne et une autre pour visualiser la vitesse angulaire.

Imposer au modèle multiphysique la valeur de la consigne permettant de simuler la vitesse 3.
Lancer la simulation sur une durée de 1 seconde.
Dans la fenêtre des variables faire un double clic sur la valeur de la consigne pour afficher la courbe.

Développer la variable vitesse et glisser déposer-la sur le graphique précédent afin de voir les deux courbes sur le même graphe.
Relever et reporter ci-dessous les valeurs des graduations.



Compléter les graduations de l'axe des ordonnées
Relever sur le graphique ci-dessus
- Consigne :
- valeur finale :
- erreur statique : Es=
- temps de réponse à ±5% : Calcul des limites haute et basse :
Quel est l’ordre de l’asservissement ?
Paramétrage du correcteur proportionnel :
Le gain proportionnel K = 10, mais l’alimentation du moteur ne peut pas dépasser 12 volts et ne peut pas descendre sous 0 volts, d’où le modèle suivant :

Quelle est l’influence de l’augmentation du gain proportionnel K1 ? quels sont les risques si K1 devient trop grand ?
Calcul des écarts entre l'attendu et la simulation
Calculer l'écart relatif entre la vitesse angulaire attendue et le simulé.
Correcteur PID
Remplacer le bloc du gain proportionnel par un bloc PID que vous trouverez dans "signal bloc" - "Controlers".

Configurer les paramètres du PID comme suit et faire les simulations sur 10s:
Téléverser les courbes dans le tableau ci-dessous.
| k=2 Ti=0.5s Td=0.1s | k=10 Ti=0.05s Td=0.1s | k=50 Ti=1s Td=0.2s |
|---|---|---|
Calcul des écarts entre l'attendu et la simulation
Calcul des écarts entre l'attendu et la mesure
Mesure de la vitesse angulaire du déplacement horizontal :
A chaque fois que le moteur effectue un tour, un capteur de fin de course s'active et passe à 5V.
Régler le berceur sur la vitesse 3.
Brancher l'oscilloscope sur le capteur de fin de course de l'interface ci-dessous et régler la base de temps de l'oscilloscope et la sensibilité de la tension afin de visualiser le signal sur une période au moins.

Déplacer les curseurs de mesure de l'oscilloscope afin de mesurer la période du signal.
Prendre une photo de l'oscillogramme de votre mesure.
Calculer la vitesse angulaire mesurée et les écarts relatifs entre l'attendu et le mesuré.
6. Etude de l’asservissement de position
Pour obtenir un bercement de type « tree swing », la vitesse de rotation du moteur vertical doit être deux fois plus grande que la vitesse de rotation du moteur horizontal. La consigne du rapport d’angle entre les deux moteurs doit donc être réglée à $(phi v)/(phi h)=2$.

Déterminer l’équation de R en fonction de φv, φh et K du modèle ci-dessus. En déduire le rôle de K=0,000001.
La simulation ci-dessous représente l’évolution de l’angle en rad des deux moteurs en fonction du temps.

D’après le graphique ci-dessus, justifiez que l’asservissement de position fonctionne bien.
Trouver un protocole de mesure permettant de vérifier que la vitesse angulaire verticale $omegav$ est 2 fois plus grande que la vitesse angulaire horizontale $omegah$. Consigner vos mesures.