SCIENCES DE L'INGENIEUR
SCIENCES DE L'INGENIEUR
Niveau : Terminale générale, enseignement de spécialité SI
D
É
C
O
N
N
E
C
T
É
Les codeurs
1 - MISE EN SITUATION
Le contrôle du déplacement, de la position ou de la vitesse d’un mobile est un problème rencontré sur un grand nombre de systèmes automatisés ou grand public (mouvements d’un robot, d’un chariot, vitesse d'une voiture ...). Les systèmes de détection conventionnels (détecteurs de position par contact ou de proximité) ne fournissent que des informations tout ou rien (TOR) ; ils ne répondent donc qu’imparfaitement au problème posé. Une des solutions consiste à utiliser un codeur optique de position.
2 - PRINCIPE DE FONCTIONNEMENT D’UN CODEUR OPTIQUE
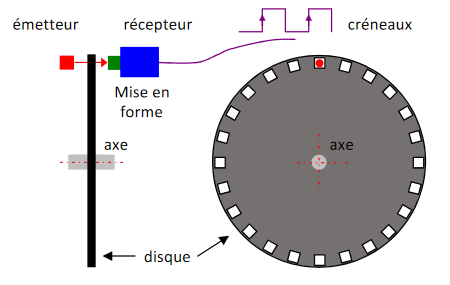
C’est un capteur de position angulaire,
- lié mécaniquement à un arbre qui l’entraîne, son axe fait tourner un disque qui lui est solidaire. Le disque comporte une succession de parties opaques et transparentes.
- une lumière émise par des Diodes Electro-
Luminescentes (DEL), traverse les fentes de ce disque
créant sur les récepteurs photoélectriques un signal
analogique
 .
. - électroniquement ce signal est amplifié puis converti
en signal carré
 , qui est alors transmis à un
système de traitement.
, qui est alors transmis à un
système de traitement.
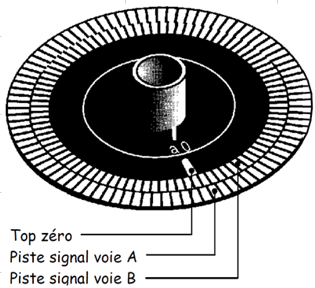
Codeur optique à impulsions et top zéro
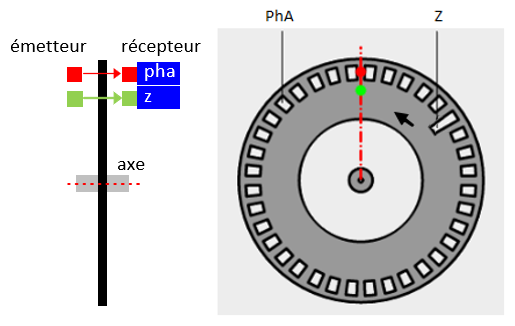
Les zones blanches laissent passer le faisceau lumineux : le niveau logique du capteur =1
Les zones grises empêchent le passage du faisceau lumineux : Le niveau logique du capteur = 0
Imaginez que le capteur est le point rouge pour pha et vert pour Z
et se trouvent sur l'axe rouge vertical et sont qu'ils sont fixes.
Faites tourner
le disque dans le sens indiqué et compléter les chronogrammes ci-dessous
(Cliquez sur le graphique pour changer l'états).

3 - UTILISATION D’UN CODEUR OPTIQUE
Les signaux carrés issus d’un codeur permettent après traitement de connaître :
- La position d’un mobile : en comptant le nombre de créneaux
- La vitesse d’un mobile : en calculant la fréquence des créneaux
- Le sens de déplacement d’un mobile : voir page suivante en fonction du type de codeur
4 - LES 2 TYPES DE CODEURS OPTIQUES
Il existe deux types de codeurs optiques :
4.1 - Le codeur incrémental
Son disque comporte en général 3 pistes (A, B, Z).
Le nombre de fenêtre de la piste A correspond à la résolution du codeur (90 points ci-dessous)
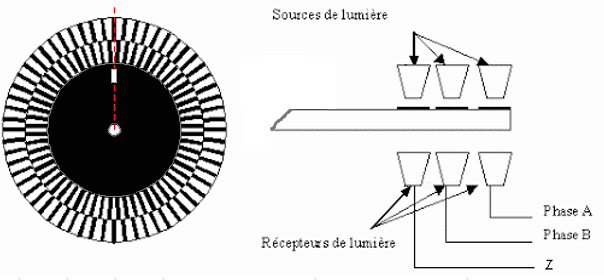
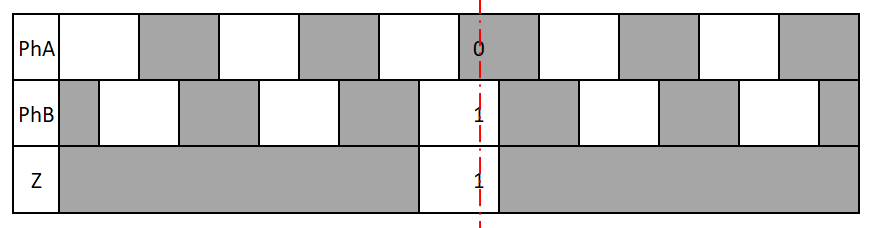
L'axe rouge reste en place PhA, PhB et Z se déplacent vers la gauche lorsque le disque tourne dans le sens anti-horaire.
Complétez les chronogrammes à partir du 2ème état (n°2), sachant que le niveau de départ (n°1) est celui de l'axe
Cette fois, le disque tourne dans le sens horaire, les signaux Pha, PhB et Z se déplacent vers la droite.
Complétez les chronogrammes ci-dessous
En observant les fronts montants de phA et le niveau logique de PhB, indiquez comment déterminer le sens de rotation du disque
4.2 - Codeurs optique Absolu
Son disque peut comporter un grand nombre de piste.
Le codage des pistes est soit en binaire naturel soit en binaire réfléchi (ou code de gray)
Code binaire réfléchi
L'axe rouge est fixe, dans quel sens tourne le disque,
afin d'obtenir l'ordre de la table de vérité ci-contre
| Ph | g | f | e | d | c | b | a |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 3 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 5 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 6 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 7 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 9 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 10 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 11 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 12 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 13 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 14 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 15 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| ... | Etc .. |
||||||
| 126 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 127 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Code binaire (naturel)
L'axe rouge est fixe, dans quel sens tourne le disque,
afin d'obtenir l'ordre de la table de vérité ci-contre
| Ph | g | f | e | d | c | b | a |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 4 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 6 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 7 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 8 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 10 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 11 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 12 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 13 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 14 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 15 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| ... | Etc ... |
||||||
| 98 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 99 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
5 - PRÉCISION D'UN CODEUR
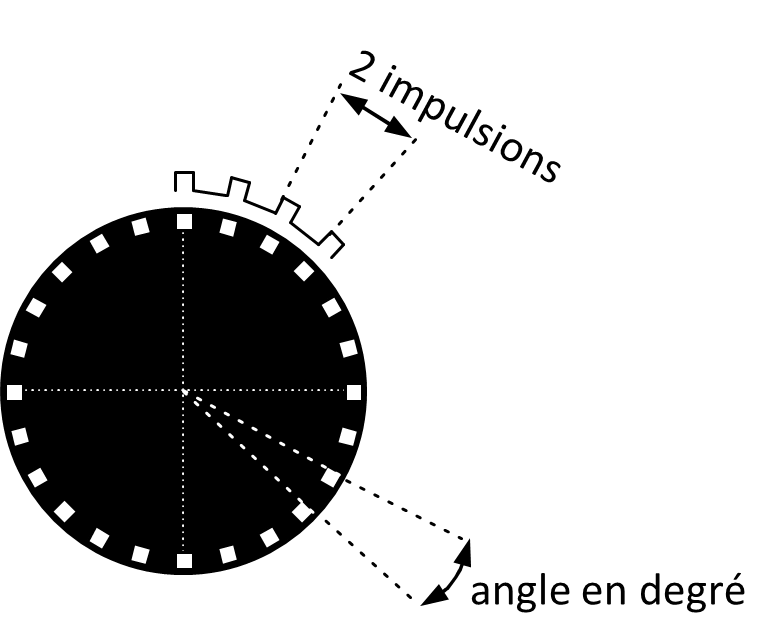
La précision d’un codeur correspond à la plus petite variation de position détectable entre deux impulsions (pour un codeur incrémental) ou entre deux secteurs (pour un codeur absolu).
5.1 - Précision rectiligne d’un mobile :
Dans le cas d’un déplacement linéaire, la précision dépend de la conversion du mouvement de rotation en mouvement de translation. Elle prend donc en compte le rayon des roues ou des poulies, ainsi que la présence éventuelle d’un réducteur.
Calcul la précision : $P = d/N$
- P : précision linéaire (en mètres)
- d : déplacement total (en mètres)
- N : nombre d’impulsions générées sur ce déplacement
Exemple : déplacement horizontal d’un chariot dans un magasin automatique
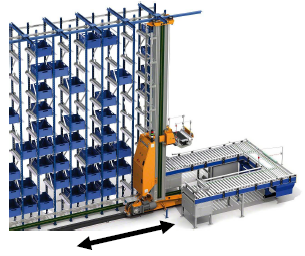
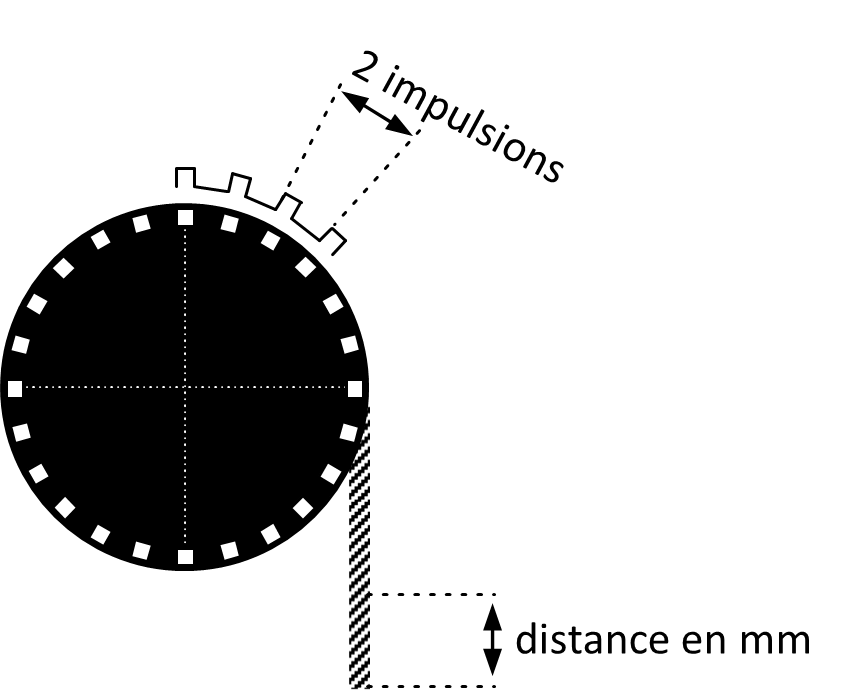
Si le capteur génère 250 impulsions lorsque le chariot se déplace de 0.5m, sa précision est :
$P=0.5/250=0.002$ m
Soit une précision de 2mm.
5.2 - Précision angulaire :
La précision angulaire correspond à la plus petite variation d’angle détectable entre deux impulsions pour un codeur incrémental, ou entre deux secteurs pour un codeur absolu.
Elle tient également compte de la présence éventuelle d’un réducteur, qui améliore la précision en sortie.
Calcul la précision : $P = theta/N$
- P : précision angulaire (en degrés)
- θ : angle parcouru (en degrés)
- N : nombre d’impulsions générées pendant ce mouvement
Exemple : Rotation d’un télescope astronomique pour suivre une planète
Le capteur du télescope VLT (Very Large Telescope) au Chili génère 900 000 impulsions pour un déplacement de 0,5° :
- $P=0.5/900000 = 0.000000556$ °
Soit une précision de 5.56$xx10^-7$ degrés.
Exercices
Exercice 1 : Système ABS d'une moto
Le système d’antiblocage des freins permet de freiner sans perdre l’adhérence et ainsi de réduire les distances de freinage tout en maîtrisant sa trajectoire.
C’est un élément de sécurité essentiel d’une voiture ou d’une moto.
La photo montre le disque de frein, son disque ABS et son capteur.

Le disque ABS est composé de 120 dents métalliques réparties toute sa circonférence. Il est fait de métal.
Q1. La moto peu rouler par n’importe quelles conditions météorologiques. Quel type de capteur est-il préférable d’installer sur la moto ?
Q2. La moto possède une roue d’un diamètre de 0.6m. Calculer sa circonférence, puis la précision du déplacement rectiligne en mm.
Q3. Si le motard roule à 30 m.s-1 (108 km.h-1) combien d’impulsions par seconde délivrera le codeur ?
Remarque : Le nombre d'impulsions générées chaque seconde, correspond aussi à la fréquence en Hertz du signal électrique généré par le codeur.
Q4. Calculer la période du signal électrique délivrée par le codeur.
Q5. Sachant que le système abs est installé sur les deux roues de la moto, expliquer comment on peut détecter le blocage de l'une d'entre elles.
Exercice 2

Calculez la résolution du codeur incrémental, en points par tour, nécessaire pour obtenir une précision linéaire d’environ 2 mm.
À quelle fréquence (nombre d'impulsions par secondes), le codeur délivre-t-il les impulsions lorsque le système se déplace à une vitesse de 0,1 m.s-1 ?
Exercice 3

Un codeur absolu binaire comporte 8 pistes, ce qui correspond à une résolution de 28 = 256 points par tour. Ce codeur est monté sur un moteur entraînant une poulie, via un réducteur.
Q1. Combien de tours effectue la poulie pour un tour complet du moteur, en tenant compte du réducteur ?
Q2. Quel est le déplacement linéaire de la courroie (en mm) pour un tour du moteur.
Q3. Calculer la précision de déplacement linéaire.
Q4. Le codeur absolu délivre la valeur binaire suivante : 0b 0101 0010. De quelle distance s’est déplacée la courroie depuis la position zéro ?
Exercice 4 : projecteur lyre

Le projecteur peut tourner sur lui-même de 360°. Un codeur absolu binaire, ayant une résolution de 1024 points/tour, permet de connaître sa position angulaire.
Q1. Calculer la précision angulaire
Q2. On suppose que la position 0° renvoie le mot binaire 0b00 0000 0000 déterminer le mot binaire à atteindre pour déplacer la lyre de 45°.
Q3. Le codeur renvoie le mot hexadécimal 0x1D3. Déterminez la position angulaire du la lyre.
Exercice 5 : Télescope Astrolab.


L'étude portera sur le contrôle du déplacement horizontal (Azimut) de l'angle de rotation de l'embase du télescope Astrolab.
Le système possède un codeur incrémental à quadrature pour contrôler l'angle.

Chronogrammes de sortie du codeur :
Q1. Parmi les tables logiques suivantes, quelle fonction correspond au chronogramme ci-dessus ?
Fonction ET
ENCA
ENCB
S = ENCA x ENCB
0 0 0 0 1 0 1 0 0 1 1 1
Fonction OU
ENCA
ENCB
S = ENCA + ENCB
0 0 0 0 1 1 1 0 1 1 1 1
Fonction OU Exclusif
ENCA
ENCB
S = ENCA ⊕ ENCB
0 0 0 0 1 1 1 0 1 1 1 0
Q2. En tenant compte du nombre d'encoches du disque, déterminer la résolution du capteur : nombre d'impulsions N à l'état haut de la sortie S pour 1 tour.
Le rapport de réduction global (roues dentées et vis sans fin) est égal à 1 : 12320
Q3. En prenant en compte le rapport de réduction, déterminez le nombre de tours que le moteur doit effectuer pour que le télescope effectue une rotation complète de 360°. En déduire ensuite le nombre d’impulsions Ni générées par le codeur pendant ce déplacement.
Q4. Calculer la précision en degré.
Q5. Le compteur du codeur s’incrémente (+1) lors d’une rotation dans le sens trigonométrique et se décrémente dans le sens inverse. Sachant que la valeur du compteur est passée de 50 000 à 40 000, déterminez les positions initiale et finale, puis en déduire l’angle parcouru ainsi que le sens de rotation.
Le système d’antiblocage des freins permet de freiner sans perdre l’adhérence et ainsi de réduire les distances de freinage tout en maîtrisant sa trajectoire. C’est un élément de sécurité essentiel d’une voiture ou d’une moto.
La photo montre le disque de frein, son disque ABS et son capteur.

Le disque ABS est composé de 120 dents métalliques réparties toute sa circonférence. Il est fait de métal.
Q1. La moto peu rouler par n’importe quelles conditions météorologiques. Quel type de capteur est-il préférable d’installer sur la moto ?
Q2. La moto possède une roue d’un diamètre de 0.6m. Calculer sa circonférence, puis la précision du déplacement rectiligne en mm.
Q3. Si le motard roule à 30 m.s-1 (108 km.h-1) combien d’impulsions par seconde délivrera le codeur ?
Remarque : Le nombre d'impulsions générées chaque seconde, correspond aussi à la fréquence en Hertz du signal électrique généré par le codeur.
Q4. Calculer la période du signal électrique délivrée par le codeur.
Q5. Sachant que le système abs est installé sur les deux roues de la moto, expliquer comment on peut détecter le blocage de l'une d'entre elles.
Calculez la résolution du codeur incrémental, en points par tour, nécessaire pour obtenir une précision linéaire d’environ 2 mm.
À quelle fréquence (nombre d'impulsions par secondes), le codeur délivre-t-il les impulsions lorsque le système se déplace à une vitesse de 0,1 m.s-1 ?
Un codeur absolu binaire comporte 8 pistes, ce qui correspond à une résolution de 28 = 256 points par tour. Ce codeur est monté sur un moteur entraînant une poulie, via un réducteur.
Q1. Combien de tours effectue la poulie pour un tour complet du moteur, en tenant compte du réducteur ?
Q2. Quel est le déplacement linéaire de la courroie (en mm) pour un tour du moteur.
Q3. Calculer la précision de déplacement linéaire.
Q4. Le codeur absolu délivre la valeur binaire suivante : 0b 0101 0010. De quelle distance s’est déplacée la courroie depuis la position zéro ?

Le projecteur peut tourner sur lui-même de 360°. Un codeur absolu binaire, ayant une résolution de 1024 points/tour, permet de connaître sa position angulaire.
Q1. Calculer la précision angulaire
Q2. On suppose que la position 0° renvoie le mot binaire 0b00 0000 0000 déterminer le mot binaire à atteindre pour déplacer la lyre de 45°.
Q3. Le codeur renvoie le mot hexadécimal 0x1D3. Déterminez la position angulaire du la lyre.


L'étude portera sur le contrôle du déplacement horizontal (Azimut) de l'angle de rotation de l'embase du télescope Astrolab.
Le système possède un codeur incrémental à quadrature pour contrôler l'angle.

Chronogrammes de sortie du codeur :
Q1. Parmi les tables logiques suivantes, quelle fonction correspond au chronogramme ci-dessus ?
Fonction ET
| ENCA | ENCB | S = ENCA x ENCB |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Fonction OU
| ENCA | ENCB | S = ENCA + ENCB |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Fonction OU Exclusif
| ENCA | ENCB | S = ENCA ⊕ ENCB |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Q2. En tenant compte du nombre d'encoches du disque, déterminer la résolution du capteur : nombre d'impulsions N à l'état haut de la sortie S pour 1 tour.
Le rapport de réduction global (roues dentées et vis sans fin) est égal à 1 : 12320
Q3. En prenant en compte le rapport de réduction, déterminez le nombre de tours que le moteur doit effectuer pour que le télescope effectue une rotation complète de 360°. En déduire ensuite le nombre d’impulsions Ni générées par le codeur pendant ce déplacement.
Q4. Calculer la précision en degré.
Q5. Le compteur du codeur s’incrémente (+1) lors d’une rotation dans le sens trigonométrique et se décrémente dans le sens inverse. Sachant que la valeur du compteur est passée de 50 000 à 40 000, déterminez les positions initiale et finale, puis en déduire l’angle parcouru ainsi que le sens de rotation.
Contenu
sous licence CC BY-NC-SA 3.0
Pascal Hassenforder 12/11/2020
MAJ : 19/04/2025