 TP -
Chapitre 7 : Algorithmes de tri et complexité
TP -
Chapitre 7 : Algorithmes de tri et complexité
N.B. Niveau : Première Générale, enseignement de spécialité NSI (Numérique et Sciences Informatiques)
D
É
C
O
N
N
E
C
T
É
Sommaire
- Recherche d’un élément d’une liste non triée
- Complexité d'un algorithme
- Recherche d'un élément dans une liste triée
- Complexité d'une recherche dans une liste triée :
- Tri d'une liste
- 5.1 - Tri par sélection du minimum
- 5.2 - Complexité du tri par sélection du minimum
- 5.3 - Tri par insertion
- 5.4 - Complexité du tri par insertion
- 5.5 - Exercice 4
- 5.6 - Exercice 5
- Insertion d'un élément dans une liste triée :
- Les invariants de boucle
Chapitre 7 - Algorithmes de tri et complexité
1 - Recherche d’un élément d’une liste non triée :
On dispose d'un jeu de 10 cartes numérotées de 1 à 10. On mélange le paquet de 10 cartes, puis on en dispose 7, faces cachées devant vous
Où se trouve la carte ? A quelle position se trouve-t-elle ?
 |
 |
 |
 |
 |
 |
 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
Algorithme employé pour trouver la carte demandée
On parcourt les cartes en commençant par la première jusqu'à la dernière Si la carte sélectionnée est la même que la carte qu'on recherche On retourne l'indice (sa position) On retourne -1 lorsque la carte n'existe pas
Exercice 1 :
Ecrire la fonction recherche_carte qui prend en paramètres une liste cartes et une variable carte_recherchee et qui retourne l'indice de la carte recherchée dans la liste des cartes si elle existe, sinon la fonction retourne -1
Compléter le programme ci-dessous en langage Python. Les cartes seront représentées par la liste [3,1,10,8,4,5,9] ci-dessous, mais on pourrait prendre n'importe quelle autre liste d'entiers.
Testez ce programme pour différentes valeurs de cartes à rechercher.
2 - Complexité d'un algorithme
La notion de complexité d'un algorithme représente l'efficacité de cet algorithme.
Nous allons étudier uniquement la complexité en temps qui est liée au nombre d'opérations élémentaires qui doivent être exécutées afin de résoudre un problème donné.
L'évaluation de ce nombre d'opérations élémentaires n'est pas chose facile, on rencontre souvent des cas litigieux.
Exemple avec : " la carte 2 se trouve-t-elle dans les cartes posées ?"
Il y a 2 cas à traiter :
- L'entier recherché est bien présent dans le tableau,
- L'entier recherché n'est pas présent dans le tableau.
| n+1 fois n fois 0 fois 1 fois |
pour n
variant de 0 à (nombre de cartes) si cartes[n] est celle qu’on recherche alors retourne n retourne -1 |
On remarque que c’est n+1 fois
On dira que la complexité
de cet algorithme est en
O(n).
Si nous avions eu n²+3n+2 nous aurions O(n²)....

3 - Recherche d'un élément dans une liste triée
Choisir 7 cartes prises au hasard parmi les 13 disponibles et classer-les par ordre croissant.
Déposez-les, face cachée sur la table, de gauche à droite.
Rechercher l'algorithme qui permet de trouver (ou pas), le  en 3 fois maximum.
en 3 fois maximum.
 |
 |
 |
 |
 |
 |
 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
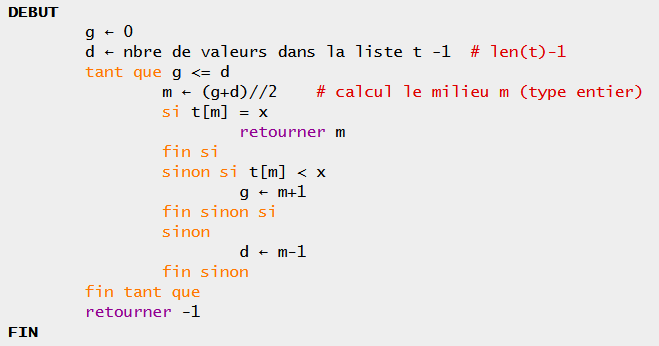
algorithme de recherche dichotomique :
Fonction recherche_dichotomique d'une valeur dans une liste triée Retourne la position de la valeur dans la liste ou -1 si elle n'y est pas paramètres : t : liste x : entier à rechercher Résultat : retourne un entier qui correspond à la position de x dans la liste t début de la fonction définir la variable g à 0 d est égal à l'indice du dernier élément de la liste t tant que g ≤ d m ← (g+d)÷2 on calcule l'indice du mileu, ATTENTION m doit être un entier si t[m] = x retourner m sinon si t[m] < x g ← m+1 sinon d ← m-1 retourner -1 fin de la fonction
On suppose que la liste t = [1,3,4,6,7,8,10] et que la carte
à rechercher est x=4 (indice 2 de la liste)
Exemple :
| Nb tests | g≤d |
m |
t[m] |
t[m]=4 ? | t[m]<4 ? | g
|
d
|
retourne |
| - |
- |
- |
- |
- |
0 |
6 |
- |
|
| 1 |
vrai |
3 |
6 |
faux |
faux |
0 |
2 |
- |
| 2 |
vrai |
1 |
3 |
faux |
vrai |
2 |
2 |
|
| 3 |
vrai |
2 |
4 |
vrai |
- |
2 |
Faire la simulation avec x=9 dans la
même liste t = [1,3,4,6,7,8,10]
| Nb tests
|
g≤d | m |
t[m] |
t[m]=9 ? | t[m]<9 ? | g |
d |
retourne |
| - |
- |
- |
- | - | - | |||
| 1 |
||||||||
| 2 |
||||||||
| 3 |
||||||||
| 4 |
4 - Complexité d'une recherche dans une liste triée :
Dans le pire des cas : c'est à dire lorsque la valeur ne se trouve
pas dans la liste, pour 7 éléments triés il faut 4 tests de
l'instruction while g≤d
Plus généralement pour n éléments dans la liste il faudra : log2(n) + 1
log2 est la fonction mathématique qui calcule le logarithme en base 2 (binaire) d'une valeur : c'est la fonction inverse de 2n
0
Exemple : si on a 256
éléments dans une liste, il faudra log2(256) + 1 = 9 tests :
On dit que la complexité est en O(log n)
: c'est ce qu'on peut avoir de mieux comme complexité.

Conclusion : pour minimiser
le temps de recherche des valeurs, il est préférable de trier les
valeurs dans un premier temps, puis de faire une recherche dichotomique.
Exercice 2 :
Traduire l'algorithme en langage python et ajouter un compteur permettant
d'indiquer le nombre de fois que la boucle while s'est exécutée.
Tester la fonction en l'appelant avec le code suivant :
print(recherche_dichotomique([i for i in range(65536)],int(input('valeur à rechercher'))))
5 - Tri d'une liste
5.1 - Tri par sélection du minimum
Algorithme
DEBUT Pour la première carte, jusqu'à l'avant dernière Mémoriser la position de cette carte qui est pour le momment la position du minimum Pour la carte suivante jusqu'à la dernière Si on trouve une carte plus petite Mémoriser la position du minimum Passer à la carte suivante Lorsqu'on arrive à la dernière carte, Echanger la première carte tirée avec celle se trouvant à la position du minimum Recommencer en prenant la carte suivante Les cartes sont triées FINAlgorithme informatique :
Fonction tri_selection_minimum d'une liste t de n éléments
Retourne une liste triée par ordre croissant
paramètres :
t : liste
Résultat :
retourne t : la liste triée
DEBUT
n ← longueur(t)
Pour i variant de 0 à n-1
indice_du_min ← i
Pour j variant de i+1 à n
Si t[j] < t[indice_du_min]
indice_du_min ← j
# Echanger t[i] et t[indice_du_min]
t[indice_du_min],t[i] ← t[i],t[indice_du_min] Retourner t
FIN
5.2 - Complexité du tri par sélection du minimum
Pour déterminer la complexité de cet algorithme, on se rend compte que l’opération qui va être faite le plus de fois est : si t[j] < t[indice_du_min]
| i | j | Nb total pour chaque j |
|---|---|---|
| 0 | 1 à n | n-1 |
| 1 | 2 à n | n-2 |
| 2 | 3 à n | n-3 |
| ... | ... | ... |
| n-3 | n-2 à n | 2 |
| n-2 | n-1 à n | 1 |
| Soit un total de 1+2+...+(n-3)+(n-2)+(n-1) =$n*(n-1)/2$ | ||
Pour n très grand $n*(n-1)/2$ ≃ $n^2/2$ donc on dira que la complexité
est en O(n²).
Exercice 3 : Traduire
l'algorithme en langage python et ajouter un compteur permettant
d'indiquer le nombre de fois que la boucle for s'est exécutée.
Tester
la fonction avec les différentes listes, puis re-testez avec 10000 valeurs Conclusion : la complexité est toujours égale à $n^/2$ quel que soit la liste à trier
5.3 - Tri par insertion :
Algorithme
DEBUTAlgorithme informatique :
Pour la 2ème carte jusqu'à la dernière
Tant que la carte en cours est inférieure aux cartes précédentes
Décaler ces dernières d'un rang vers la droite
Fin tant que
poser la carte tirée à sa place
prendre la carte suivante
Fin pour
FIN
Fonction tri_insertion d'une liste t de n éléments
Retourne une liste triée par ordre croissant avec un tri par insertion
paramètres :
t : liste
Résultat :
t : liste triée
DEBUT
L ← longueur(t)
Pour i variant de 1 à L
en_cours ← t[i]
j ← i-1
Tant que j>=0 et en_cours < t[j]
t[j+1] ← t[j]
j ← j-1
Fin tant que
t[j+1] ← en_cours
Fin Pour
Retourner t
FIN
5.4 - Complexité du tri par insertion :
Pour déterminer la complexité de cet algorithme, on se rend compte que l’opération qui va être faite le plus de fois est : tant que j ≥ 0.
On suppose que le tableau est trié dans le sens inverse (pire des cas)
| i | j | Nb total pour chaque j |
|---|---|---|
| 1 | 0 à -1 | 1 |
| 2 | 1 à -1 | 2 |
| 3 | 2 à -1 | 3 |
| ... | ... | ... |
| n-2 | n-3 à -1 | n-2 |
| n-1 | n-2 à -1 | n-1 |
| Soit un total de 1+2+...+(n-3)+(n-2)+(n-1) =$((n+2)*(n-1))/2$ | ||
Pour n très grand $((n+2)*(n-1))/2$ ≃ $n^2/2$ donc on dira que la complexité est en O(n²).
Dans le meilleur cas, lors d'une liste déjà triée, la complexité sera en O(n).
5.5 - Exercice 4 :
Traduire l'algorithme en langage python et ajouter un compteur permettant d'indiquer le nombre de fois que la boucle while s'est exécutée. Tester avec des listes triées croissantes, décroissantes et non triées. Comparez les deux méthodes.
5.6 - Exercice 5 :
Tests sur un fichier csv contenant la liste des presque 400 communes du Haut-Rhin et leur code postal
Fichier non trié : laposte.csv Fichier trié : laposteT.csvPlacer le code ci-dessous dans l'exercice 4 et vérifier que le tri fonctionne.
Pour vérifier la complexité, on peut aussi mesurer le temps du tri. Celui-ci varie légèrement à cause des processus qui tournent en parallèle sur l'ordinateur.
Triez uniquement les 50 premières communes de la liste : t= tri_insertion(t[0:50]), puis 100 et 200. Le temps moyen mesuré, doit augmenter proportionnellement à $n^2/2$.
On peut imaginer le temps que mettra l'ordinateur à trier les quelques 35000 communes de France
Vérifier la complexité sur le fichier trié : laposteT.csv
6 - Insertion d'un élément dans une liste triée :
La méthode la plus efficace est de rechercher la position ou devra être placé l'élément à insérer en utilisant l'algorithme de recherche dichotomique.
Exemple : t=[1,3,4,6,7,8,10] l'élément à insérer est x=5 qui doit s'insérer à l'indice 3 dans la liste t
On va former une nouvelle liste formée des éléments de t d'indices 0 à 3, de l'élément x et des éléments de t d'indices 3 à la fin
t = [1,3,4] + [5] + [6,7,8,10]Si la variable pos est égal au retour de la fonction de recherche_dichotomique(t,x),
- alors
t = t[:pos]+[x]+t[pos:]Exercice 6 :
Ajouter la possibilité d'insérer la ville et son code postal "MULHOUSE;68059", dans la liste lue depuis depuis le fichier "laposteT.csv", puis l'afficher le résultat dans la console. Vous utiliserez la fonction recherche_dichotomique(t,x) dont le code ci-dessous a été adapté à la situation et qui retournera l'indice d'insertion de l'élément x
Essayer l'insertion d'une ville au premier rang puis au dernier rang.
Quelle est la complexité de l'algorithme ?
Instagram dénombre près d'un milliard d'utilisateurs actifs (1 000 000 000). Avec l'algorithme précédent, en combien d'occurrences est-on capable d'insérer un nouvel utilisateur ?
Remarque sur l'utilisation
de la mémoire de l'ordinateur : si on prend une moyenne de 8 lettres
pour stocker rien que les identifiants des utilisateurs d'Instagram,
il faudrait 8 Go de mémoire pour stocker et manipuler ces données...
Expliquer que fait le programme suivant et en déduire sa compléxité
7 - Les invariants de boucle
A priori, les algorithmes de tri par insertion et de tri par sélection "fonctionnent" correctement, on dit que ces algorithmes sont corrects.
Il se pourrait très bien que dans une situation donnée notre algorithme ne donne pas le résultat attendu.
Il existe un moyen de démonter la correction d'un algorithme. Si nous arrivons à démontrer la correction de l'algorithme de tri, nous pourrons alors affirmer que, quel que soit le tableau donné en entrée, nous obtiendrons bien en sortie ce même tableau, mais trié.
Pour démontrer la correction de l'algorithme de tri par insertion, il faut utiliser un "invariant de boucle"
On appelle invariant de boucle, une propriété qui est vraie avant et après chaque itération.
La démonstration doit se faire en 3 étapes :
- INITIALISATION : on doit montrer que l'invariant de boucle est vrai avant la première itération de la boucle
- CONSERVATION : on doit montrer que si l'invariant de boucle est vrai avant une itération de la boucle, il le reste avant l'itération suivante.
- TERMINAISON : une fois la
boucle terminée, l'invariant fournit une propriété utile qui aide à
montrer la correction de l'algorithme.
Prenons un exemple : le tri par insertion :
DEBUT
L ← longueur(t)
Pour i variant de 1 à L
en_cours ← t[i]
j ← i-1
Tant que j>=0 et en_cours < t[j]
t[j+1] ← t[j]
j ← j-1
Fin tant que
t[j+1] ← en_cours
Fin Pour
Retourner t
FIN
On suppose que t=[6,4,5,1,9]
|
i |
en_cours |
Liste
avant prochaine itération de i |
|
Initialisation
i=0 |
6 4 5 1 9 |
|
|
1 |
4 |
4
6 5 1 9 |
|
2 |
5 |
4
5 6 1 9 |
|
3 |
1 |
1
4 5 6 9 |
|
4 |
6 |
1
4 5 6 9 |
A chaque itération de i (de la boucle pour), nous devons montrer que le tableau t[0….i] est trié : c’est l’invariant de boucle.
- INITIALISATION : on a i=1 donc t[0..1] ne comporte qu’un élément, il est forcément trié.
- CONSERVATION : si on regarde l’algorithme, on déplace tous les éléments vers la droite tant que l’élément i est plus petit que l’élément j (jusqu’à ce que l’on trouve la bonne place dans la partie triée) donc forcément le nouveau tableau t[0…i] est trié puisque t[0 .. 1] est trié, t[0…2] le sera et ainsi de suite jusqu’à t[0….i].Donc l’invariant le tableau t[0….i] est trié avant est vrai et le reste après chaque itération.
- TERMINAISON : la boucle
se termine, i = L donc notre tableau est t[0….L] qui correspond au
tableau d’origine mais trié.
Cette démonstration nous permet d'affirmer que l'algorithme de tri par insertion est correct, mais ne prouve pas qu'il est juste...
Capsule réalisée par Cédric GERLAND Lycée Saint-Exupéry, Nantes-la-Jolie
Fond : Texte : Tables : Thème du langage:
?>
Contenu
sous licence CC BY-NC-SA 3.0
Pascal Hassenforder - Gisèle Bareux 08/05/2021
MAJ : 29/01/2025