NUMERIQUE ET SCIENCES INFORMATIQUES

Niveau : 1ère générale, enseignement de spécialité NSI

 
Chapitre 1 : Représentation des données Chapitre 2 : Logique combinatoire et séquentielle Chapitre 3 : Les réseaux : adresses IP Chapitre 4 - Interactions entre l’homme et la machine Chapitre 5 - Les formulaires sur le web Chapitre 6 - Machine learning - KNN Chapitre 7 - Algorithmes gloutons
 
Chapitre 1 - Variables, types et opérateurs Chapitre 2 - Les conditions (instructions if, elif, else) Chapitre 3 - Les boucles (instructions for, while) Chapitre 4 - Les fonctions Chapitre 5 - Mini projet Jeu Chapitre 6 - Communiquer en réseau Chapitre 7 - Algorithmes et complexité Chapitre 8 - Système d'exploitation Linux Chapitre 9 - Jeu codé de nim en php Chapitre 10 - Jeu du 2048 codé en Javascript
 
TP Chapitre 1 TP Chapitre 2 TP Chapitre 3 TP Chapitre 4
 

D
É
C
O
N
N
E
C
T
É

Chapitre 6 : Machine learning - KNN

1 -Introduction :

Le Machine Learning est un ensemble de techniques permettant de créer, à partir de données, des modèles prédictifs qui apprennent par eux-mêmes. L'ordinateur va s'entrainer sur un jeu de données dont il connait les résultats et sera ensuite capable de résoudre un problème par lui-même.

Ces machines utilisent bien entendu des algorithmes qui permettent par exemple de vous suggérer des amis sur les réseaux sociaux.  

2 - Algorithme des K plus proche voisins (KNN)

Dis-moi qui sont tes voisins, je te dirai qui tu es.

Exemple : classer différents types d’IRIS :

Nous allons utiliser le jeu de données d'Anderson, du nom d'Edgar Anderson qui en 1936 a collecté des données de 3 espèces d'iris :"iris setosa", "iris virginica" et "iris versicolor". Il a mesuré (en cm) :

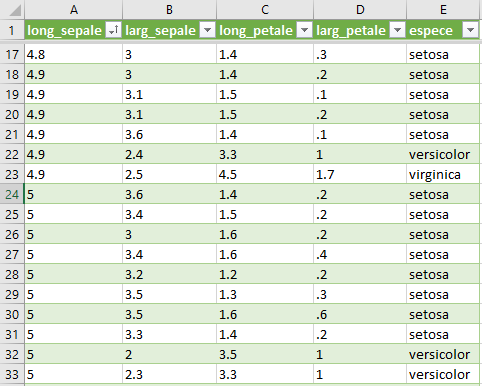iris Fichier scv

Toutes ces données ont été stockées dans un fichier csv qui pourra être lu par une machine.

Pour cette partie, il faut commencer par récupérer le fichier iris.csv

Mettre à jour edupython avec la version 2.7 qui prend en charge la bibliothèque pandas : Edupython2.7

Dans un premier temps, nous allons afficher un graphique qui en abscisse représente la longueur des pétales, en ordonnée la largeur des pétales et une couleur par espèce (vert pour setosa, rouge pour viriginica et bleu pour versicolor) pour cela nous utiliserons la bibliothèque matplotlib.

Pour faire le graphique, il faut d’abord charger le fichier csv pour récupérer les données. Nous allons utiliser la bibliothèque pandas (import pandas).

# Affichage des données du fichier iris.csv  
import matplotlib.pyplot as plt
import pandas

donnees = pandas. read_csv ('iris.csv', header =0)	# lecture du fichier iris.csv 

setosa = donnees[donnees['espece'] == 'setosa']		# setosa contiendra la liste des meures de toutes les espèces d'iris 'setosa' 
plt . scatter ( setosa ['long_sepale'], setosa ['larg_sepale'],color='g', label ='setosa')	# abscisse : long_petale, ordonnée : larg_petale , color green 

plt.xlabel ('longeur sepale')	# affichage des label 
plt.ylabel ('largeur sepale')
plt.title ('Iris')		# titre 
plt.legend ();			# légende des label 
plt.show() 			# affiche le graphique

Exercice 1 :

Modifier le programme afin d'afficher le graphique des largeurs et longueurs des pétales toutes les espèces permettant d'obtenir le graphique suivant :

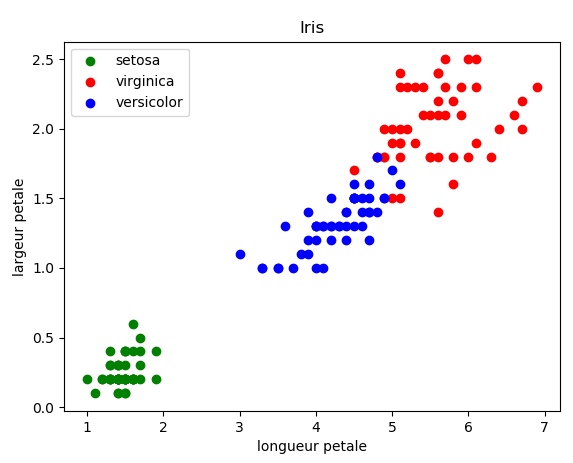
graph1

Collez votre code python dans la fenêtre ci-dessous puis cliquez sur enregistrer:


La répartition des points permet de voir que l'espèce setosa est vraiment différente et éloignée des autres espèces, donc facilement différenciable. Par-contre, les iris virginica et versicolor ont des longueurs et largeurs de pétales similaires, des points se mélangent.

Imaginez qu'au cours d'une promenade vous tombiez nez à nez avec un iris. Vous n'êtes pas un spécialiste des iris mais vous souhaiteriez connaître l'espèce. Vous mesurez les dimensions des pétales suivantes : longueur 2cm et largeur 0.5 cm.Faire apparaître ce nouveau point, avec une couleur noire (color='k'), dans le graphique afin de voir à quelle espèce il appartient.

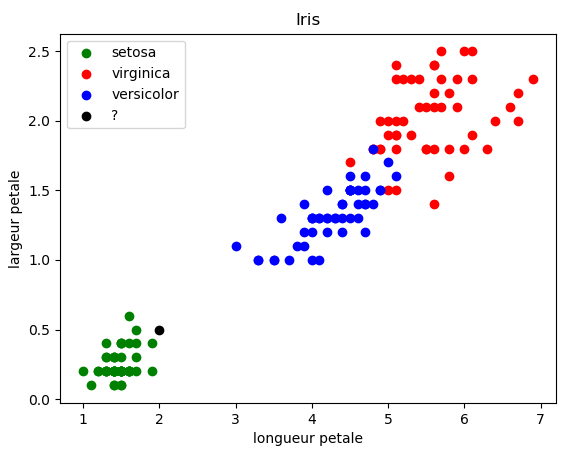
graph2

Sans aucun doute, l'iris trouvé fait partie de l'espèce setosa. Mais qu'en est-il de l'iris ayant les mesures suivantes : longueur = 2,5 et largeur=0.75


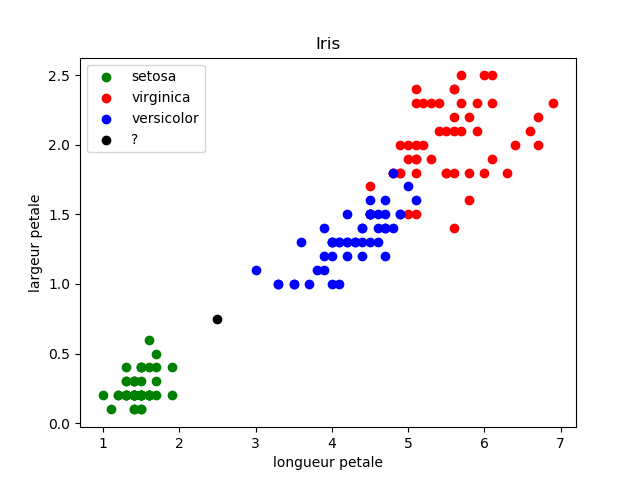
graph 3

Dans ce genre de cas, il peut être intéressant d'utiliser l'algorithme des "k plus proches voisins", en quoi consiste cet algorithme :

Prenons k = 3

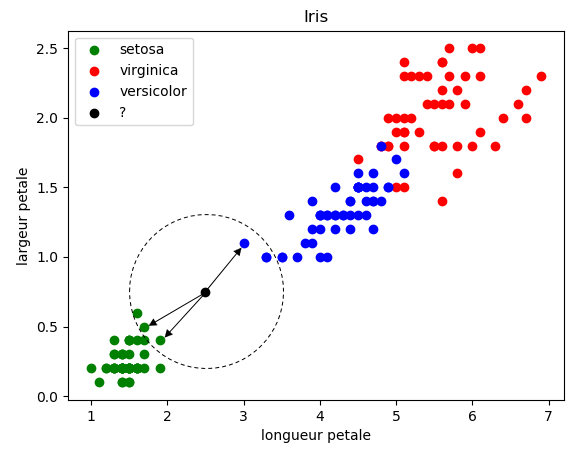
graph 4

Les 3 plus proches voisins sont signalés ci-dessus avec des flèches : nous avons deux "iris setosa" (point vert) et un "iris virginica" (point bleu). D'après l'algorithme des "k plus proches voisins", notre "iris mystère" appartient à l'espèce "setosa".

La bibliothèque Python Scikit Learn propose un grand nombre d'algorithmes liés au machine learning (c'est sans aucun doute la bibliothèque la plus utilisée en machine learning). Parmi tous ces algorithmes, Scikit Learn propose l'algorithme des k plus proches voisins.

Programme du KNN

étudiez et testez le code suivant :

# Recherche des k plus proches voisins  
import matplotlib.pyplot as plt
import pandas
from sklearn.neighbors import KNeighborsClassifier

#traitement CSV
donnees = pandas. read_csv ('iris.csv', header =0)
x=donnees.loc[:,"long_petale"]
y=donnees.loc[:,"larg_petale"]
lab=donnees.loc[:,"espece"]

# Valeurs mesurées:
long_petale=2.5
larg_petale=0.75
k=3

setosa = donnees[donnees['espece'] == 'setosa']
virginica = donnees[donnees['espece'] == 'virginica']
versicolor = donnees[donnees['espece'] == 'versicolor']

plt.scatter(setosa ['long_petale'], setosa ['larg_petale'],color='g', label ='setosa')
plt.scatter(virginica ['long_petale'], virginica ['larg_petale'],color='r', label ='virginica')
plt.scatter(versicolor ['long_petale'], versicolor ['larg_petale'],color='b', label ='versicolor')

# algorithme KNN

d=list(zip(x,y))
model = KNeighborsClassifier(n_neighbors=k)
model.fit(d,lab)
prediction= model.predict([[long_petale,larg_petale]])

#Affichage résultats

plt.xlabel('longueur petale')
plt.ylabel('largeur petale')
plt.title('Iris')
plt.legend();

plt.scatter(long_petale,larg_petale,color='k',label=prediction)

txt="Résultat : " + prediction[0]
plt.text(3,0.5, "largeur : " + str(larg_petale) + " cm longueur : " + str(long_petale)+ " cm", fontsize=12)
plt.text(3,0.3, "k : " + str(k), fontsize=12)
plt.text(3,0.1, txt, fontsize=12)
#fin affichage résultats

plt.show()
Analyse du programme :

la ligne "d=list(zip(x,y))" permet de passer de 2 listes x et y 

x = [1.4, 1.4, 1.3, 1.5, 1.4, 1.7, 1.4, ...]

y = [0.2, 0.2, 0.2, 0.2, 0.2, 0.2, 0.4,....]

à une liste de tuples contenant (x,y) de chaque iris

d = [(1.4, 0.2), (1.4, 0.2), (1.3, 0.2) (1.5, 0.2), (1.4, 0.2), (1.7, 0.2), (1.4, 0.4), ...]

"KNeighborsClassifier" est une méthode issue de la bibliothèque scikit-learn (voir plus haut le "from sklearn.neighbors import KNeighborsClassifier"), cette méthode prend ici en paramètre le nombre de "plus proches voisins" (model = KNeighborsClassifier(n_neighbors=k))

"model.fit(d, lab)" permet d'associer les tuples présents dans la liste "d" avec les labels (0 : setosa, 26 : setosa, 120 : virginica ...). Par exemple le premier tuple de la liste "d", (1.4, 0.2) est associé au premier label de la liste lab (0), et ainsi de suite...  

   lab     lab   

La ligne "prediction= model.predict([[longueur,largeur]])" permet d'effectuer une prédiction pour un couple [longueur, largeur] (dans l'exemple ci-dessus "longueur=2.5" et "largeur=0.75"). 

La variable "prediction" contient alors le label trouvé par l'algorithme knn. Attention, "predection" est une liste Python qui contient un seul élément (le label), il est donc nécessaire d'écrire "predection[0]" afin d'obtenir le label.

>>> print(prediction)
['setosa']
>>> print(prediction)[0]
'setosa'

Vous devriez normalement obtenir ceci :

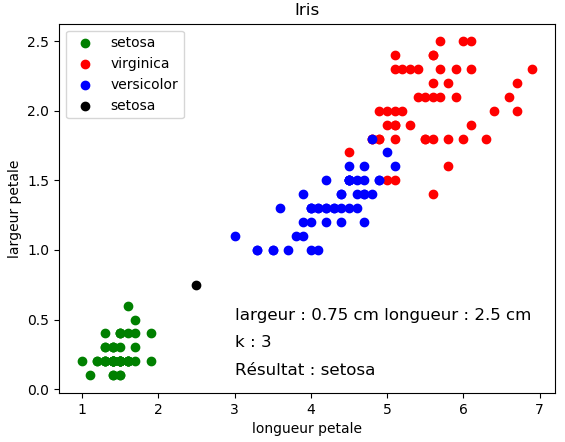
graph5

Exercice 2 :

Modifiez le programme afin de tester l'algorithme knn avec un nombre "de plus proches voisins" différent (en gardant un iris ayant une longueur de pétale égale à 2,5 cm et une largeur de pétale égale à 0,75 cm). Que se passe-t-il pour k = 5 ?

Testez l'algorithme knn avec un iris de votre choix en inventant des mesures de pétales.

Notez dans la fenêtre ci-dessous les résultats des prédictions et les tests réalisés pour différentes valeurs de k et d'iris


prise en compte de la largeur des sépales et affichage 3D

import matplotlib.pyplot as plt
import numpy as np
import pandas
from sklearn.neighbors import KNeighborsClassifier
from mpl_toolkits.mplot3d import axes3d

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

#traitement CSV
donnees = pandas. read_csv ('iris.csv', header =0)
x=donnees.loc[:,"long_petale"]
y=donnees.loc[:,"larg_petale"]
z=donnees.loc[:,"larg_sepale"]
lab=donnees.loc[:,"espece"]

# Valeurs mesurées:
long_petale=2.5
larg_petale=0.75
larg_sepale=2
k=3

setosa = donnees[donnees['espece'] == 'setosa']
virginica = donnees[donnees['espece'] == 'virginica']
versicolor = donnees[donnees['espece'] == 'versicolor']

ax.scatter3D(np.array([list(setosa ['long_petale'])],dtype=np.float),np.array([list(setosa ['larg_petale'])],dtype=np.float),np.array([list(setosa ['larg_sepale'])],dtype=np.float),label='setosa')
ax.scatter3D(np.array([list(virginica ['long_petale'])],dtype=np.float), np.array([list(virginica ['larg_petale'])],dtype=np.float),np.array([list(virginica['larg_sepale'])],dtype=np.float),label='virginica')
ax.scatter3D(np.array([list(versicolor ['long_petale'])],dtype=np.float), np.array([list(versicolor ['larg_petale'])],dtype=np.float),np.array([list(versicolor['larg_sepale'])],dtype=np.float),label='versicolor')

# algorithme KNN
d=list(zip(x,y,z))
model = KNeighborsClassifier(n_neighbors=k)
model.fit(d,lab)
prediction= model.predict([[long_petale,larg_petale,larg_sepale]])
print (prediction[0])

#Affichage résultats
ax.scatter3D(np.array([[long_petale]],dtype=np.float), np.array([[larg_petale]],dtype=np.float),np.array([[larg_sepale]],dtype=np.float),label=prediction[0])
ax.legend()
ax.set_xlabel('longueur petale')
ax.set_ylabel('largeur petale')
ax.set_zlabel('largeur sepale')
ax.text2D(-0.05,0.095,"Résultat : "+ prediction[0], fontsize=12)
ax.legend()

#fin affichage résultats
plt.show()

Exercice :

Sans modifier l'affichage 3D (compréhension 4D délicate : avec un bargraphe), écrire le script permettant de prendre en compte les 4 caractéristiques des iris : la longueur et la largeur des sépales ainsi que des pétales. Vous pouvez prendre des valeurs déjà existantes dans le fichier CSV pour vérifier s'il retrouve la bonne espèce.

Collez votre code python dans la fenêtre ci-dessous puis cliquez sur enregistrer:


Fond : Texte : Tables :