NUMERIQUE ET SCIENCES INFORMATIQUES
NUMERIQUE ET SCIENCES INFORMATIQUES
Niveau : Terminale générale, enseignement de spécialité NSI
D
É
C
O
N
N
E
C
T
É
Fractales récursives
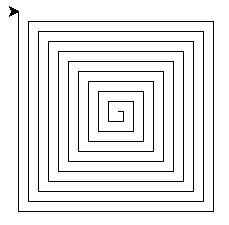
Exercice 1Réaliser à l’aide d’une fonction récursive le dessin suivant :
| un colimaçon |
|---|
 |
Cahier des charges
- L'arrêt de la fonction récursive ce fait lorsque la longueur L < 5
- La longueur maximale sera égale à 200
- A chaque récursion on réduit la longueur de 5
- Le module turtle qui permet de dessiner les lignes
Principales fonctions du module turtle
| • goto(x,y) | Aller à l'endroit de coordonnées x et y |
| • forward(distance) | Avancer d'une distance donnée |
| • backward(distance) | Reculer |
| • up() | Relever le crayon (pour pouvoir avancer sans dessiner) |
| • down() | Abaisser le crayon (pour pouvoir recommencer à dessiner) |
| • color(couleur) | Couleur peut être une chaîne prédéfinie ('red', 'blue', 'green', etc.) |
| • left(angle) | Tourner à gauche d'un angle donné (exprimé en degré) |
| • right(angle) | Tourner à droite |
| • width(épaisseur) | Choisir l'épaisseur du tracé |
| • write(texte) | texte doit être une chaîne de caractères délimitée avec des " ou des ' |
| • speed(vitesse) | Définit la vitesse de traçage (vitesse est un entier compris entre 0 à 9) |
| Résultat |
|---|
Exercice 2 : ★★
| l'arbre binaire |
|---|
 |
Cahier des charges
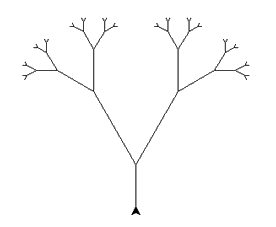
- Le tronc qui aura une longueur de 50 se fait avant la déclaration de la fonction.
- La condition d'arrêt se fait lorsque la longueur de la branche est inférieure à 5
- L'angle entre les branches est de 30° et la longueur de la première branche est égale à 100
- La longueur de la seconde branche et des branches suivantes seront divisées par 2
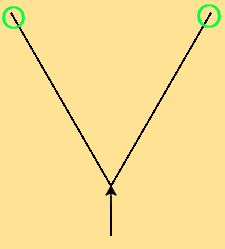
Pour résoudre le problème, on commence par dessiner uniquement 2 branches à partir du tronc :
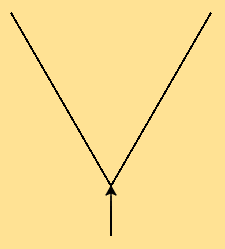
Lorsqu'on atteint les extrémités des branches (en vert) on appelle récursivement la fonction avec L/2
| Résultat |
|---|
Exercice 3 : ★★
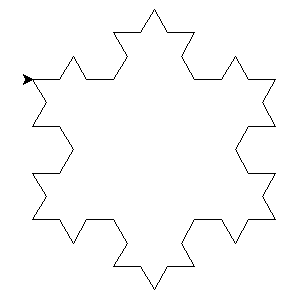
| Le flocon de Koch |
|---|
 |
| Ordre 0 | Ordre 1 | ordre 2 |
|---|---|---|
 |  | 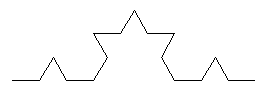 |
Cahier des charges
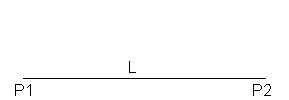
- L'ordre 0 sera notre condition de sortie et est composée d'un segment de Longueur L
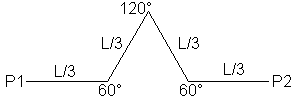
- L'ordre 1 est composé du motif d'ordre 0 de longueur L/3
- L'ordre 2 est composé du motif d'ordre 1 de Longueur L/3
- L'ordre 3 est composé du motif d'ordre 2 de Longueur L/3
Généralisation
A partir de l'ordre 1, l'ordre n est composé du motif de l'ordre n-1 de longueur L/3
Programmer le motif de l'ordre 0 lorsque n=0 sinon le motif d'ordre 1 appelant le motif d'ordre n-1 avec une longueur L/3
| Résultat |
|---|
Exercice 4 : ★★
| Le triangle de Sierpinzki |
|---|
 |
| Ordre 0 | Ordre 1 | ordre 2 |
|---|---|---|
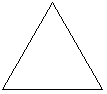 | 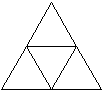 | 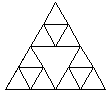 |
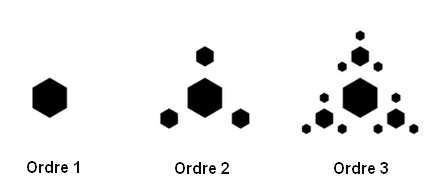
- L'ordre 0 sera notre condition de sortie et est composée d'un triangle de Longueur L
- L'ordre 1 est composé de 3 triangles d'ordre 0 de longueur L/2
- L'ordre 2 est composé de 3 triangles d'ordre 1 de Longueur L/2
- L'ordre 3 est composé de 3 triangles d'ordre 2 de Longueur L/2
Généralisation
A partir de l'ordre 1, l'ordre n est composé du motif de l'ordre n-1 de longueur L/2
Programmer le triangle d'ordre 0 de longueur L, puis les 3 triangles d'ordre 1, en appelant l'ordre n-1.
Le dessin des triangles commence en bas à gauche. Vous pouvez vous aider d'un crayon et d'une feuille de papier pour dessiner l'ordre 1
| Résultat |
|---|
Exercice 5 : ★
Écrire en Python une procédure (non récursive) carre qui :
- prend en paramètre une variable taille,
- trace un carré centré au point où se situe la tortue au moment d'appeler la procédure et de côté taille,
- replace la tortue à sa position et dans son orientation de départ
| Carré |
|---|
 |
| Résultat |
|---|
Exercice 6 : ★★
Copier la fonction carre et en faire une fonction récursive fractale_carre qui :
- prend en paramètre un entier taille et un entier profondeur strictement positif,
- trace une fractale carrée (voir ci-dessous) à l'aide de (profondeur - 1) couches d'appels récursifs et dont le plus grand carré a pour côté taille et la taille des petits carrés sont divisés par 3
- Replace la tortue à sa position et dans son orientation de départ
| Ordre 0 | Ordre 1 | Ordre 2 |
|---|---|---|
 | 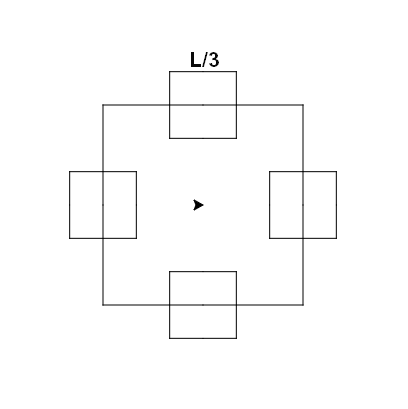 | 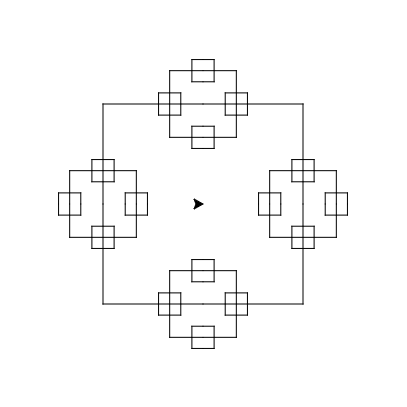 |
| Résultat |
|---|
Exercice 7 : ★★