NUMERIQUE ET SCIENCES INFORMATIQUES

Niveau : Terminale générale, enseignement de spécialité NSI

Les arbres

Auteur : Van Zuijlen Stéphan CC BY-NC

☰

Somaire

1. Introduction
2. Notions générales sur les arbres.
   • Représentations graphiques
   • Définitions
   • Exercice
3. Les arbres binaires
   • Introduction
   • Comment représenter un arbre binaire...à la main...
   • Exercice 1
   • Programmation de l'arbre
   • Une seconde façon de faire...
   • Exercice 2
   • Calcul de la hauteur de l'arbre
4. Les parcours
   • Les parcours en largeur
   • Simulation de l'algorithme
   • Les parcours en profondeur
   • définitions
5. Utilisation d'une classe
   • Exercice 3 :

1 - Introduction

Nous rencontrons souvent des schémas qui permettent de mettre en évidence une structure sur des données.

Par exemple : Ce schéma se suffit à lui même pour qui prend la peine de le lire...

De même pour le très classique arbre généalogique

Voici un arbre syntaxique: Un arbre syntaxique représente l’analyse d’une phrase à partir de règles (la grammaire).

Arbre lexicographique : Un arbre lexicographique, ou arbre en parties communes, ou dictionnaire, représente un ensemble de mots. Les préfixes communs à plusieurs mots apparaissent une seule fois dans l’arbre.

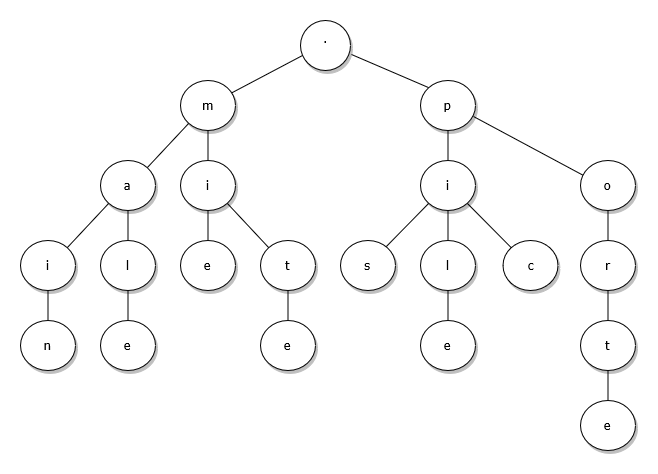
Cliquez sur l'image de l'arbre ci-dessus

Editer le diagramme en cliquant sur le crayon

Ajoutez dans l'arbre lexicographique les mots : malle et portail.

donnez aux 2 mots une couleur différente

Cliquez sur Fichier - Exporter en tant que - SVG... puis Exporter, Télécharger

On peut également représenter les expressions arithmétiques par des arbres étiquetés par des opérateurs, des constantes et des variables. La structure de l’arbre rend compte de la priorité des opérateurs et rend inutile tout parenthésage. Pour l’expression : (y÷2−t)(75 +z) cela donne :

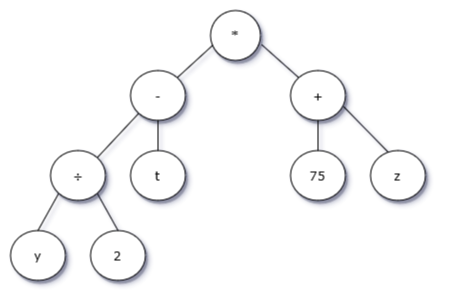
Représenter l’expression : 3 + (7÷3 - 1)³

Les arbres sont très utilisés en informatique, d’une part parce que les informations sont souvent hiérarchisées et peuvent se représenter naturellement sous une forme arborescente, et d’autre part, parce que les structures de données arborescentes permettent de stocker des données volumineuses de façon que leur accès soit efficace.

2 - Notions générales sur les arbres.

On peut considérer un arbre comme une généralisation d’une liste car les listes peuvent être représentées par des arbres. Plutôt que de chercher à définir ce qu’est un arbre, nous observerons quelques schémas.

Voici les représentations graphiques :

d’un arbre

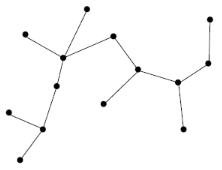
une forêt

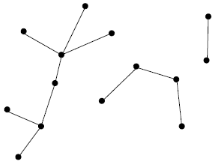
Attention : Ceci n’est pas un arbre, car il existe un chemin d’un sommet vers lui même (appelé un cycle).

Lorsqu’un sommet se distingue des autres, on le nomme racine de l’arbre et celui-ci devient alors une arborescence (par la suite on utilisera le mot arbre pour une arborescence).

Les 3 arbres ci-dessus représentent la même structure, cependant pour deux d’entre eux, un sommet peut être désigné comme racine. On a l’habitude, lorsqu’on dessine un arbre, de le représenter avec la tête en bas, c’est-à-dire que la racine est tout en haut, et les nœuds fils sont représentés en-dessous du nœud père

Définitions

Étiquette :

Un arbre dont tous les nœuds sont nommés est dit étiqueté. L’étiquette (ou nom du sommet) représente la "valeur" du nœud ou bien l’information associée au nœud.

Ci-dessous, un arbre étiqueté avec les entiers entre 1 et 10.

Racine, nœud, branche, feuille :

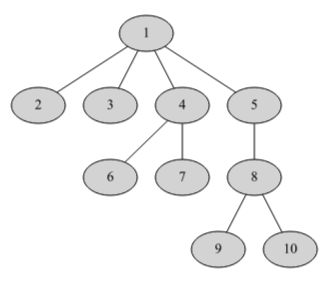
Un arbre est un ensemble organisé de nœuds dans lequel chaque nœud a un père, sauf un nœud que l’on appelle la racine. Si le nœud n’a pas de fils, on dit que c’est une feuille.Les nœuds sont reliés par des branches.

Hauteur d’un nœud :

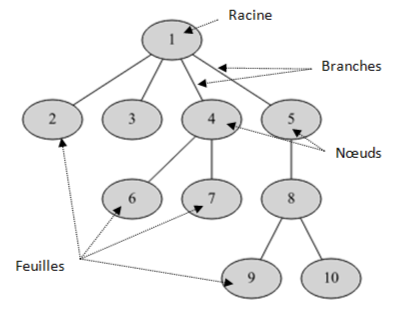
la hauteur (ou profondeur ou niveau) d’un nœud X est égale au nombre d’arêtes qu’il faut parcourir à partir de la racine pour aller jusqu’au nœud X.

Par convention, la hauteur (ou profondeur)de la racine est égale à 0 (Attention : La définition de la hauteur d’un nœud varie en fonction des auteurs. Pour certains la racine a une hauteur de 1.)

Dans l’exemple ci-contre la hauteur du nœud 9 est de 3 et celle du nœud 7 est de 2.

La hauteur (ou profondeur) d’un arbre est égale à la profondeur du nœud le plus profond.

Dans notre exemple, le nœud le plus profond est de profondeur 3, donc l’arbre est de profondeur 3

Taille d’un arbre :

La taille d’un arbre est égale au nombre de nœuds de l’arbre

Dans notre exemple, l’arbre contient 10 nœuds, sa taille est donc de 10.

Degré d’un nœud, degré d’un arbre :

Le degré d’un nœud est égal au nombre de ses descendants (enfants). Le degré d’un arbre est égal au plus grand des degrés de ses nœuds

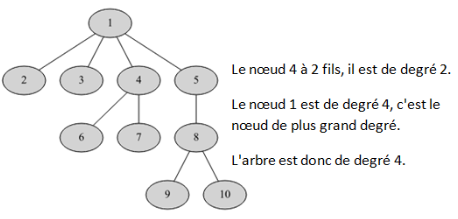
Remarques :

Le vocabulaire de lien entre nœuds de niveaux différents et reliés entres eux est emprunté à la généalogie.

Dans notre exemple :

• 8 est le parent de 9 et de 10
• 6 est un enfant de 4
• 6 et 7 sont des nœuds frères
• 5 est un ancêtre de 9
• 10 est un descendant de 5

Un arbre dont tous les nœuds n’ont qu’un seul fils est en fait une liste.

Exercice :

Dans l'arbre ci-dessous, déterminez :

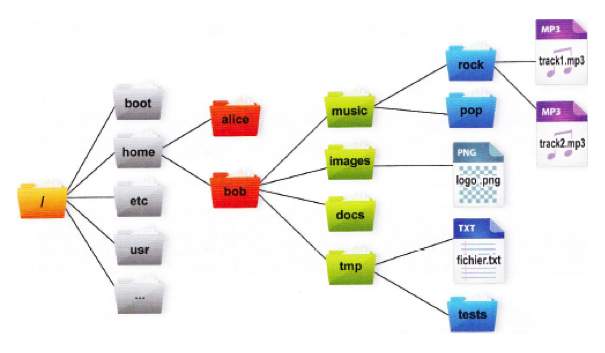
	la taille :
	la hauteur :
	le degré de Bob :
	3 feuilles :
	les fils de tmp :
	le parent de music :
	un ancêtre de docs :
	un descendant de bob :

3 - Les arbres binaires

Introduction

Parmi la forêt d’arbres possibles, on s’intéressera essentiellement aux arbres dit binaires : Un arbre binaire est un arbre de degré 2 (dont les noeuds sont de degré 2 au plus).

Vocabulaire :

Les enfants d’un nœud sont lus de gauche à droite et sont appelés : fils gauche et fils droit.

Définition :

L’arbre qui représente l’expression a×b+c−(d+e) est un arbre binaire

Les arbres binaires forment une structure de données qui peut se définir de façon récursive.

Un arbre binaire est :

• Soit vide.
• Soit composé d’une racine portant une étiquette (clé) et d’une paire d’arbres binaires, appelés sous-arbres gauche et droit

Les arbres binaires sont utilisés dans de très nombreuses activités informatiques, nous allons étudier et implanter cette structure de données

Comment représenter un arbre binaire...à la main...

L’idée est de représenter l’arbre avec un tableau :

La racine suivie de ses fils gauche et droit.

r

a

b

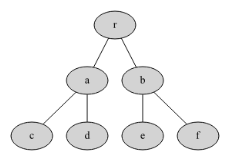
Puis on rajoute dans l’ordre les fils gauche et droit de a, puis ceux de b.

r

a

b

c

d

e

f

Remarque :

Chaque nœud se repère par son indice n dans la liste, son fils gauche se trouvant alors à l’indice 2*n + 1 et son fils droit à l’indice 2*n + 2.

Exemple :

Le nœud "b" est à l’indice n=2 son fils gauche se trouve alors à l’indice 5 et son fils droit à l’indice 6.

Si un nœud n’a pas de fils on le précise en mettant ’None’ à sa place. Notre arbre est alors représenté par le tableau : ['r','a','b','c','d','e','f',None,None,None,None,None,None,None,None]

Quelle taille doit avoir le tableau ?

Cet arbre est complet (tous les noeuds in-ternes ont deux fils). Il possède 3 niveaux, sa hauteur ou profondeur est donc de 2.

Donc la taille du tableau sera de : 2⁰+ 2¹+ 2²+ 2³= 2⁴−1 = 15

il faut compter le nombre de noeuds, y compris les noeuds "fantômes" des feuilles

Exercice 1 :

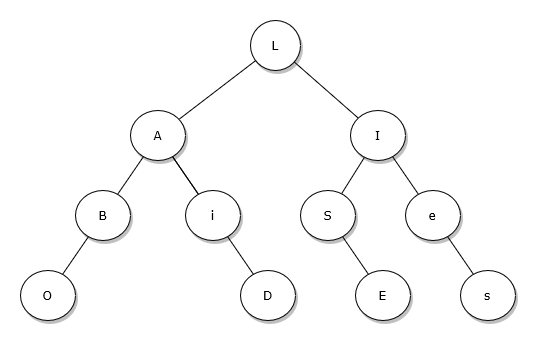
Quelle devra être la taille du tableau ?

Écrire le tableau représentant cet arbre :

Quelle propriété ont les indices des fils gauches et droits ?

Voici un tableau représentant un arbre binaire : ['*','-',5,2,6,None,None,None,None,None,None,None,None,None,None]

Que peut il représenter ?

Voici un code Python qui crée la liste représentant l’arbre de l’exercice 1 :

def Creation_arbre(r,profondeur): ''' r : la racine (str ou int). la profondeur de l’arbre (int)''' Arbre = [r]+[None for i in range(2**(profondeur+1)-2)] return Arbre def Insertion_noeud(arbre,noeud,fg,fd): '''Insére les noeuds et leurs enfants dans l’arbre''' n = arbre.index(noeud) arbre[2*n+1] = fg arbre[2*n+2] = fd # création de l’arbre arbre = Creation_arbre('L',4) # ajout des noeuds par niveau de gauche à droite Insertion_noeud(arbre,'L','A','I') Insertion_noeud(arbre,'A','B','i') Insertion_noeud(arbre,'I','S','e') Insertion_noeud(arbre,'B','O',None) Insertion_noeud(arbre,'i',None,'D') Insertion_noeud(arbre,'S',None,'E') Insertion_noeud(arbre,'e',None,'s') #pour vérifier print('Taille du tableau',len(arbre)) print('Arbre=',arbre) ''' # Tests des fonctions à venir : dépalcer les triples cotes print('Arbre vide :',Arbre_vide(arbre)) noeud='I' print(Enfants(arbre,noeud),'sont les enfants de',noeud) print(Fils_gauche(arbre,noeud),'est le fils gauche') print(Fils_droit(arbre,noeud),'est le fils droit') print(noeud,'est racine :',Racine(arbre,noeud)) print(noeud,'est une feuille :',Est_feuille(arbre,noeud)) print(Parent(arbre,noeud),'est le parent de',noeud) print(noeud,'a un frère :',Frere(arbre,noeud)) '''

Exécuter

Créer les fonctions suivantes :

• Une fonction Arbre_vide(arbre) qui retourne vrai si l’arbre est vide.
• Une fonction Enfants(arbre,noeud) qui retourne les enfants d'un noeud sous la forme d'un uplet (fg,fd).
• Deux fonctions Fils_gauche(arbre,noeud) qui retournent le fils gauche d’un noeud et son homologue Fils_droit(arbre,noeud) s’ils existent.
• Une fonction Racine(arbre,noeud) qui retourne vrai si le noeud est la racine de l’arbre.
• Une fonction Est_feuille(arbre,noeud) qui retourne vrai si le noeud est une feuille.
• Une fonction Parent(arbre,noeud) qui retourne le parent du noeud ou False si c'est la racine
• Une fonction Frere(arbre,noeud) qui retourne vrai si le noeud a un frère gauche ou droit
• Testez plusieurs noeuds avec une boucle pour et une liste de noeud=['I','L','O','S']

Aides :

• Un arbre vide ne contient que des None.
• n = arbre.index(noeud) permet de trouver l'indice n du noeud dans la liste arbre.
• Exemple : si arbre = ['L', 'A', 'I', 'B', 'i'...] en exécutant le code n = arbre.index('B') alors n sera égal à 3.
• Connaissant l'indice n du noeud, on pourra facilement trouver l'indice du fils gauche et droit (formule du cours).
• fg=2*n+1 est une équation si on recherche le parent (n), il faut isoler la variable n de l'équation. Attention l'indice n doit toujours être un entier.
• Si le noeud est une feuille, ses deux enfants sont None.
• Les indices des fils gauches ou droits on une propriété particulière citée plus haut dans le cours plus haut.

Résulat souhaité :

Arbre vide : False
Taille du tableau 31
Arbre= ['L', 'A', 'I', 'B', 'i', 'S', 'e', 'O', None, None, 'D', None, 'E', None, 's', None, None, None, None, None, None, None, None, None, None, None, None, None, None, None, None]
('S', 'e') sont les enfants de I
S est le fils gauche
e est le fils droit
I est racine : False
I est une feuille : False
L est le parent de I
I a un frère : True
('A', 'I') sont les enfants de L
A est le fils gauche
I est le fils droit
L est racine : True
L est une feuille : False
False est le parent de L
L a un frère : False
(None, None) sont les enfants de O
None est le fils gauche
None est le fils droit
O est racine : False
O est une feuille : True
B est le parent de O
O a un frère : False
(None, 'E') sont les enfants de S
None est le fils gauche
E est le fils droit
S est racine : False
S est une feuille : False
I est le parent de S
S a un frère : True

Une seconde façon de faire...

Comme vous l’avez sans doute constaté, il est assez fastidieux de représenter un arbre avec un unique tableau surtout pour un arbre très profond. L’idée est de représenter l’arbre avec un tableau contenant des tableaux

Cet arbre se représente par le tableau:[’r’,[’a’,[],[]],[’b’,[],[]]]

Exercice 2 :

Écrire le tableau représentant cet arbre

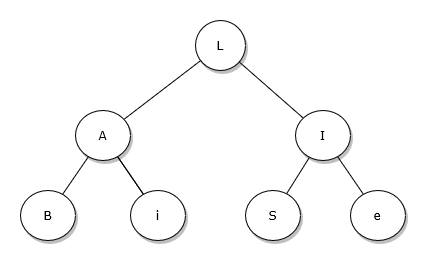
Le code Python ci-dessous, construit l’arbre de l’exercice 2 de manière récursive.

• Les noeuds sont représentés par un dictionnaire.
• L’arbre se construit depuis la racine en construisant les sous-arbres des fils gauche et droit.

def Noeud(nom, fg =None, fd =None) : return {'racine': nom, 'fg' : fg, 'fd': fd} # création des noeuds e = Noeud('e') S = Noeud('S') i = Noeud('i') B = Noeud('B') I = Noeud('I',S,e) A = Noeud('A', B,i) racine = Noeud('L', A, I) # création de l'arbre def Construit(arbre) : if arbre ==None: return[] else: return[arbre['racine'],Construit(arbre['fg']),Construit(arbre['fd'])] # gestion de pile et file def empiler(donnee,pile): pile.append(donnee) def defiler(file): return file.pop() def enfiler(donnee,file): file.insert(0,donnee) arbre=Construit(racine) print(arbre)

Exécuter

Les fonctions l'exercice 2 sont assez évidentes à écrire puisqu’on a accès directement aux noeuds.

Nous allons nous intéresser à la hauteur de l’arbre, ainsi qu’aux différentes façons de le parcourir :

• Le parcours en largeur.
• Les parcours en profondeur (parcours préfixe, parcours infixe et parcours suffixe).

Calcul de la hauteur de l’arbre :

L’idée est la suivante :

• Si l’arbre est vide la hauteur vaut -1.
• Sinon la hauteur vaut 1 auquel il faut ajouter le maximum entre les hauteurs des sous-arbres gauche et droit.
• Ces sous-arbres sont eux mêmes des arbres dont il faut calculer la hauteur.

Une méthode récursive semble tout à fait adaptée à la situation.
Voici l’algorithme

Fonction hauteur (arbre)
Paramètres : arbre binaire représenté comme tableau de tableaux [racine , [fg] , [fd] ] et fg=[noeud , [fg] , [fd] ]
Retourne un entier : la hauteur de l'arbre

	Si l’arbre est vide alors
		renvoyer -1
	Sinon
		h1←1+hauteur(arbre[1])
		h2←1+hauteur(arbre[2])
		renvoyer max(h1,h2)

Écrire cette fonction dans le code précédent et vérifier que la profondeur de l’arbre est de 2.

Mofofications

Dans le script précédent, implémenter l’arbre ci-dessous et faites calculer sa profondeur

Les parcours

Le parcours en largeur :

Le parcours d’un arbre en largeur consiste à partir de la racine on visite ensuite son fils gauche puis son fils droit, puis le fils gauche du fils gauche etc.. Comme le montre le schéma ci-dessous:

L’idée est la suivante :

On utilise une file.

• On met l’arbre dans la file.
• Puis tant que la file n’est pas vide:
• On défile la file.
• On récupère sa racine.
• On enfile son fils gauche s’il existe
• On enfile son fils droit s’il existe.

Voici l’algorithme:

Fonction Parcours_Largeur(arbre)
Paramètre : un arbre binaire
Retourne la liste des sommets d'un parcours en largeur

    f une file vide
    l une liste vide
    Pour chaque noeud dans l'arbre faire
        enfiler le noeud dans la file

    Tant quela longueur de f est >0
        defiler f dans une variable tmp
        Si la longueur de tmp >1 alors
            empiler tmp[0] dans la l
            Si tmp[1] n’est pas vide alors
                enfiler tmp[1] dans f
            Si tmp[2] n’est pas vide alors 
                enfiler tmp[2] dans f
        Sinon 
            empiler tmp dans l
    retourne l

Complétez le fichier de simulation de l'algorithme ci-dessus:

arbre = [ 'r' , ['a',[],[]] , ['b',[],[]] ]
	liste	noeud	tmp	f	longueur file >0	longueur tmp >1
f une file vide				- [] 'r' ['a',[],[]],'r' ['b',[],[]],['a',[],[]],'r' ['b',[],[]],['a',[],[]] ['b',[],[]]
liste une liste vide	- [] ['r'] ['r','a'] ['r','a','b']
pour chaque nœud dans l'arbre		- 'r' ['a',[],[]] ['b',[],[]]
enfiler le noeud dans la file				- [] 'r' ['a',[],[]],'r' ['b',[],[]],['a',[],[]],'r' ['b',[],[]],['a',[],[]] ['b',[],[]]
nœud suivant		- 'r' ['a',[],[]] ['b',[],[]]
enfiler le noeud dans la file				- [] 'r' ['a',[],[]],'r' ['b',[],[]],['a',[],[]],'r' ['b',[],[]],['a',[],[]] ['b',[],[]]
nœud suivant		- 'r' ['a',[],[]] ['b',[],[]]
enfiler le noeud dans la file				- [] 'r' ['a',[],[]],'r' ['b',[],[]],['a',[],[]],'r' ['b',[],[]],['a',[],[]] ['b',[],[]]
Tant que la longueur de la file est >0					- True False
defiler la file dans une variable tmp			- 'r' ['a',[],[]] ['b',[],[]]	- [] 'r' ['a',[],[]],'r' ['b',[],[]],['a',[],[]],'r' ['b',[],[]],['a',[],[]] ['b',[],[]]
Si la longueur de tmp >1 alors						- True False
empiler tmp[0] dans la liste	- ['r'] ['r','a'] ['r','a','b']
Tant que la longueur de la file est >0					- True False
defiler la file dans une variable tmp			- 'r' ['a',[],[]] ['b',[],[]]	- [] 'r' ['a',[],[]],'r' ['b',[],[]],['a',[],[]],'r' ['b',[],[]],['a',[],[]] ['b',[],[]]
Si la longueur de tmp >1 alors						- True False
empiler tmp[0] dans la liste	- ['r'] ['r','a'] ['r','a','b']
Tant que la longueur de la file est >0					- True False
defiler la file dans une variable tmp			- 'r' ['a',[],[]] ['b',[],[]]	- [] 'r' ['a',[],[]],'r' ['b',[],[]],['a',[],[]],'r' ['b',[],[]],['a',[],[]] ['b',[],[]]
Si la longueur de tmp >1 alors						- True False
empiler tmp[0] dans la liste	- ['r'] ['r','a'] ['r','a','b']
Tant que la longueur de la file est >0					- True False
retourne liste	- ['r'] ['r','a'] ['r','a','b']

Implémenter cette fonction dans le code du de l'exercice 2. Si vous avez bien programmé, vous pourez faire fonctionner vos ZY...

Les parcours en profondeur

On se balade autour de l’arbre en suivant les pointillés

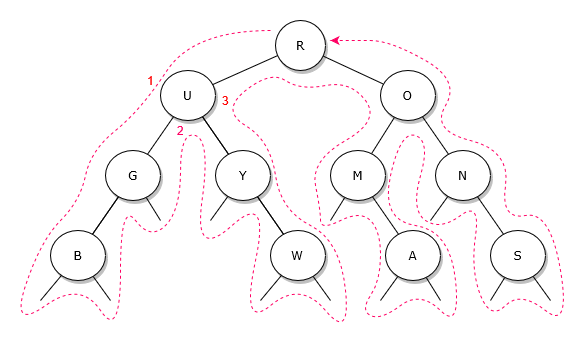
Dans le schéma ci-dessus, on a rajouté des "noeuds fantômes" pour montrer que l’on peut considérer que chaque nœud est visité 3 fois

• Une fois par la gauche.
• Une fois par en dessous.
• Une fois par la droite

On peut définir les parcours comme suit :

Dans un parcours préfixe, on liste le noeud la première fois qu’on le rencontre.

Écrire les sommets dans un parcours préfixe.

Dans un parcours infixe, on liste le noeud la seconde fois qu’on le rencontre.

Ce qui correspond à : on liste chaque noeud ayant un fils gauche la seconde fois qu’on le voit et chaque noeud sans fils gauche la première fois qu’on le voit.

Écrire les sommets dans un parcours infixe.

Dans un parcours suffixe, on note le noeud la dernière fois qu’on le rencontre.

Écrire les sommets dans un parcours suffixe.

Définition :

Voici 3 algorithmes récursifs, dire pour chacun d’entre eux à quel parcours il correspond.

Fonction Parcours_(arbre,l=list())
    Paramètres : l'arbre binaire et une liste l vide par défaut
    retourne la liste l des sommets parcourrus
	
    Si L’arbre n’est pas vide alors
        Parcours_(sous-arbre gauche,l)
        Parcours_(sous-arbre droit,l)
        Ajouter La racine de l’arbre à l
    Retourner l

Fonction Parcours_(arbre,l=list())
    Paramètres : l'arbre binaire et une liste l vide par défaut
    retourne la liste l des sommets parcourrus
	
    Si L’arbre n’est pas vide alors
        Ajouter La racine de l’arbre à l
        Parcours_(sous-arbre gauche,l)
        Parcours_(sous-arbre droit,l)
    Retourner l

Fonction Parcours_(arbre,l=list())
    Paramètres : l'arbre binaire et une liste l vide par défaut
    retourne la liste l des sommets parcourrus
	
    Si L’arbre n’est pas vide alors
        Parcours_(sous-arbre gauche,l)
        Ajouter La racine de l’arbre à l
        Parcours_(sous-arbre droit,l)
    Retourner l

Implémenter ces trois fonctions dans le ci-dessous et vérifier vos réponses des 3 questions précédentes.

def Noeud(nom, fg =None, fd =None) : return {'racine': nom, 'fg' : fg, 'fd': fd} # création des noeuds S = Noeud('S') A = Noeud('A') W = Noeud('W') B = Noeud('B') N = Noeud('N',None,S) M = Noeud('M', None, A) Y = Noeud('Y',None,W) G = Noeud('G',B,None) O = Noeud('O',M,N) U = Noeud('U', G, Y) racine = Noeud('R', U, O) # création de l'arbre def Construit(arbre) : if arbre ==None: return[] else: return[arbre['racine'],Construit(arbre['fg']),Construit(arbre['fd'])] arbre=Construit(racine)

Exécuter

Remarque : Tout ce que nous venons de faire peut être fait uniquement avec la variable racine qui est un dictionnaire représentant l’arbre de manière tout aussi efficace que la représentation par tableau de tableaux de arbre1.

Une troisième façon de faire...avec une classe

Nous allons créer une classe Noeud dont les attributs d’instances seront :

• Le nom (ou valeur) de la racine.
• Son fils gauche (vide par défaut).
• Son fils droit (vide par défaut).

De plus on rajoute une méthode spécifique, qui permet d’afficher la racine du noeud avec la fonction print()

Ci-dessous la classe Noeud et la représentation de l’arbre. (La racine possède deux fils qui sont eux mêmes des noeuds possédant deux fils qui.....)

class Noeud: # Le constructeur def __init__(self, value, left=None, right=None): self.value = value self.left = left self.right = right # Méthode qui permet d’afficher la valeur # de la racine avec la fonction print def __str__(self): return str(self.value) S = Noeud('S') A = Noeud('A') W = Noeud('W') B = Noeud('B') N = Noeud('N',None,S) M = Noeud('M', None, A) Y = Noeud('Y',None,W) G = Noeud('G',B,None) O = Noeud('O',M,N) U = Noeud('U', G, Y) arbre = Noeud('R', U, O) print (arbre) # affiche R

Exécuter

On aurait pu écrire la représentation de l’arbre sur une seule ligne...mais c’est assez compliqué de ne pas se perdre...

arbre=Noeud('R',Noeud('U',Noeud('G',Noeud('B',None,None),None),Noeud('Y',None,Noeud('W',None,None))),Noeud('O',Noeud('M',None,Noeud('A',None,None)),Noeud('N',None,Noeud('S',None,None))))

Écrire une méthode EstFeuille qui renvoie vrai si le noeud est une feuille et faux sinon.

Exercice 3 :

La hauteur de l’arbre : Reprenons notre fonction Hauteur(arbre) l'exercice 2

def hauteur(arbre): if arbre == []: return -1 else: h1 = 1 + hauteur(arbre[1]) h2 = 1 + hauteur(arbre[2]) return max(h1, h2)

Adaptons là à notre contexte :

def hauteur2(arbre): if not arbre: return -1 else: h1 = 1 + hauteur2(arbre.left) h2 = 1 + hauteur2(arbre.right) return max(h1, h2)

Rajouter cette fonction au code précédent et vérifier que la hauteur de notre arbre RUGBYWOMAN est bien 3.

Exercice 3.2

Et si on en faisait une méthode...

Généralement pour transformer une fonction en méthode, il suffit de remplacer la variable (arbre ici) par self, cependant du fait de la propriété récursive de la fonction, il faudra en plus s’assurer que les arbres gauche et droit existent.

Voici la méthode :

def hauteur(self): h1=0 h2=0 if not self: return-1 else: if self.left: h1 = 1+self.left.hauteur() if self.right: h2 = 1+self.right.hauteur() return max(h1, h2)

Exercice 3.3

Rajouter cette méthode au code précédent et tester là avec la commande : print(arbre.hauteur()).

Les parcours:

Voici les trois fonctions de parcours :

def parcours_infixe(arbre): if arbre: parcours_infixe(arbre.left) print(arbre, end=' ' ) parcours_infixe(arbre.right) def parcours_prefixe(arbre): if arbre: print(arbre, end=' ' ) parcours_prefixe(arbre.left) parcours_prefixe(arbre.right) def parcours_suffixe(arbre): if arbre: parcours_suffixe(arbre.left) parcours_suffixe(arbre.right) print(arbre, end=' ' )

Exercice 3.4 :

Transformer en méthodes ces trois fonctions.

Remarque :

Vaut-il mieux utiliser une méthode ou une fonction ?

Cela dépend en fait de ce que l’on souhaite faire, dans notre cas, si c’est juste pour afficher les parcours, les méthodes suffisent. Mais si c’est pour faire quelque chose avec les noeuds, une fonction sera plus efficace car nous pourrons stocker ces noeuds dans une liste. Comme le montre le code ci-dessous

liste_parcours_infixe=[] def parcours_infixe(arbre): if arbre: parcours_infixe(arbre.left) liste_parcours_infixe.append(arbre.value) parcours_infixe(arbre.right) return liste_parcours_infixe

Exercice 4 : Sujet 0 année 2023

A traiter sur une feuille de copie

L’exercice porte sur les arbres binaires de recherche et la programmation objet. Dans un entrepôt de e-commerce, un robot mobile autonome exécute successivement les tâches qu’il reçoit tout au long de la journée.

La mémorisation et la gestion de ces tâches sont assurées par une structure de données.

1. Dans l'hypothèse où les tâches devraient être extraites de cette structure (pour être exécutées) dans le même ordre qu’elles ont été mémorisées, préciser si ce fonctionnement traduit le comportement d’une file ou d’une pile. Justifier.

En réalité, selon l'urgence des tâches à effectuer, on associe à chacune d’elles, lors de la mémorisation, un indice de priorité (nombre entier) distinct : il n'y a pas de valeur en double.

Plus cet indice est faible, plus la tâche doit être traitée prioritairement.

La structure de données retenue est assimilée à un arbre binaire de recherche (ABR) dans lequel chaque nœud correspond à une tâche caractérisée par son indice de priorité.

Rappel :

Dans un arbre binaire de recherche, chaque nœud est caractérisé par une valeur (ici l'indice de priorité), telle que chaque nœud du sous-arbre gauche a une valeur strictement inférieure à celle du nœud considéré, et que chaque nœud du sous- arbre droit possède une valeur strictement supérieure à celle-ci. Cette structure de données présente l'avantage de mettre efficacement en œuvre l'insertion ou la suppression de nœuds, ainsi que la recherche d'une valeur.

Par exemple, le robot a reçu successivement, dans l’ordre, des tâches d’indice de priorité 12, 6, 10, 14, 8 et 13. En partant d’un arbre binaire de recherche vide, l’insertion des différentes priorités dans cet arbre donne la figure 1.

Figure 1 : Exemple d’un arbre binaire

2. En utilisant le vocabulaire couramment utilisé pour les arbres, préciser le terme qui correspond :

a. au nombre de tâches restant à effectuer, c’est-à-dire le nombre total de nœuds de l’arbre ;

b. au nœud représentant la tâche restant à effectuer la plus ancienne ;

c. au nœud représentant la dernière tâche mémorisée (la plus récente).

3. Lorsque le robot reçoit une nouvelle tâche, on déclare un nouvel objet, instance de la classe Noeud, puis on l’insère dans l’arbre binaire de recherche (instance de la classe ABR) du robot. Ces 2 classes sont définies comme suit :

class Noeud: def __init__(self, tache, indice): self.tache = tache #ce que doit accomplir le robot self.indice = indice #indice de priorité (int) self.gauche = ABR() #sous-arbre gauche vide (ABR) self.droite = ABR() #sous-arbre droit vide (ABR) class ABR: #arbre binaire de recherche initialement vide def __init__(self): self.racine = None #arbre vide #Remarque : si l'arbre n'est pas vide, racine est #une instance de la classe Noeud def est_vide(self): """renvoie True si l'arbre autoréférencé est vide, False sinon""" return self.racine == None def insere(self, nouveau_noeud): """insere un nouveau noeud, instance de la classe Noeud, dans l’ABR""" if self.est_vide(): self.racine = nouveau_noeud elif self.racine.indice ...... nouveau_noeud.indice: self.racine.gauche.insere(nouveau_noeud) else: self.racine.droite.insere(nouveau_noeud)

a. Donner les noms des attributs de la classe Noeud.

b. Expliquer en quoi la méthode insere est dite récursive et justifier rapidement qu’elle se termine.

c. Indiquer le symbole de comparaison manquant dans le test à la ligne 26 de la méthode insere pour que l’arbre binaire de recherche réponde bien à la définition de l’encadré « Rappel » de la page 6.

d. On considère le robot dont la liste des tâches est représentée par l’arbre de la figure 1. Ce robot reçoit, successivement et dans l’ordre, des tâches d’indice de priorité 11, 5, 16 et 7, sans avoir accompli la moindre tâche entretemps. Recopier et compléter la figure 1 après l’insertion de ces nouvelles tâches.

4. Avant d’insérer une nouvelle tâche dans l’arbre binaire de recherche, il faut s’assurer que son indice de priorité n’est pas déjà présent. Écrire une méthode est_present de la classe ABR qui répond à la description :

def est_present(self, indice_recherche) : """renvoie True si l’indice de priorité indice_recherche (int) passé en paramètre est déjà l’indice d’un nœud de l’arbre, False sinon"""

5. Comme le robot doit toujours traiter la tâche dont l’indice de priorité est le plus petit, on envisage un parcours infixe de l’arbre binaire de recherche.

a. Donner l’ordre des indices de priorité obtenus à l’aide d’un parcours infixe de l’arbre binaire de recherche de la figure 1.

b. Expliquer comment exploiter ce parcours pour déterminer la tâche prioritaire.

6. Afin de ne pas parcourir tout l'arbre, il est plus efficace de rechercher la tâche du nœud situé le plus à gauche de l'arbre binaire de recherche : il correspond à la tâche prioritaire.

Recopier et compléter la méthode récursive tache_prioritaire de la classe ABR:

def tache_prioritaire(self): """renvoie la tache du noeud situé le plus à gauche de l'ABR supposé non vide""" if self.racine...........est_vide():#pas de nœud plus à gauche return self.racine.......... else: return self.racine.gauche..........()

7. Une fois la tâche prioritaire effectuée, il est nécessaire de supprimer le nœud correspondant pour que le robot passe à la tâche suivante :

• Si le nœud correspondant à la tâche prioritaire est une feuille, alors il est simplement supprimé de l'arbre (cette feuille devient un arbre vide)
• Si le nœud correspondant à la tâche prioritaire a un sous-arbre droit non vide, alors ce sous-arbre droit remplace le nœud prioritaire qui est alors écrasé, même s'il s'agit de la racine.

Dessiner alors, pour chaque étape, l'arbre binaire de recherche (seuls les indices de priorités seront représentés) obtenu pour un robot, initialement sans tâche, et qui a, successivement dans l'ordre :

• étape 1 : reçu une tâche d'indice de priorité 14 à accomplir
• étape 2 : reçu une tâche d'indice de priorité 11 à accomplir
• étape 3 : reçu une tâche d'indice de priorité 8 à accomplir
• étape 4 : accompli sa tâche prioritaire
• étape 5 : reçu une tâche d'indice de priorité 12 à accomplir
• étape 6 : accompli sa tâche prioritaire
• étape 7 : accompli sa tâche prioritaire
• étape 8 : reçu une tâche d'indice de priorité 15 à accomplir
• étape 9 : reçu une tâche d'indice de priorité 19 à accomplir
• étape 10 : accompli sa tâche prioritaire