 NUMERIQUE ET SCIENCES INFORMATIQUES
NUMERIQUE ET SCIENCES INFORMATIQUES
Niveau : Terminale générale, enseignement de spécialité NSI
D
É
C
O
N
N
E
C
T
É
Les graphes
1 - La théorie des graphes :
On a des sommets et des arrêtes ou arcs si la liaison n'est pas bidirectionnelle. Les sommets de notre graphe se sont les villes, les arrêtes représentent le poids : ici, la distance séparant deux villes entre elles.
Pour aller à Mulhouse à Nancy, quel sera le chemin le plus court :
Les successeurs de Mulhouse sont : Strasbourg, Nancy, Epinal et Vesoul
Les prédécesseurs de Vesoul sont : Nancy, Epinal et Mulhouse qui
sont également ses successeurs.
Pour trouver le chemin le plus court dans ce graphe il existe
l'algorithme de Dijkstra ou Prim traité à la fin du chapitre.
1.1 - Généralités :
Les graphes sont employés par exemple par les GPS pour trouver le chemin le plus court entre deux villes
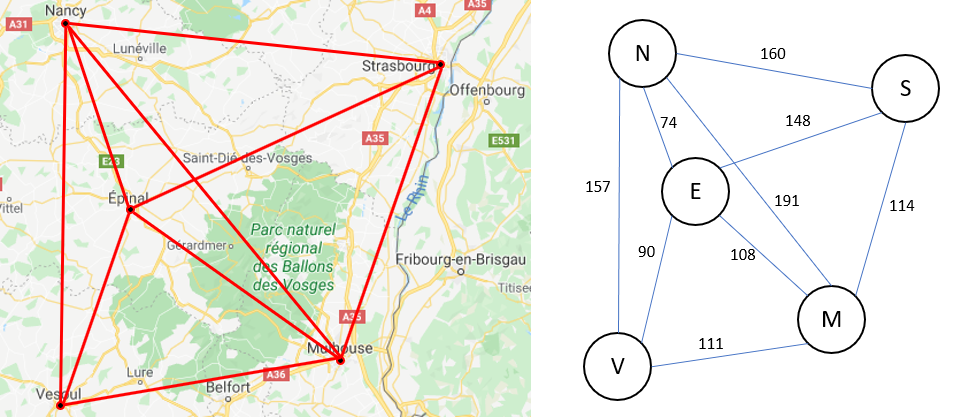
Définitions
- d'un ensemble S de sommets : les villes dans notre exemple.
- d'un ensemble A de couples d'éléments de S, appelés arcs (pour les graphes orientés) ou arêtes (pour les graphes non orientés) : les distances séparant les villes.
- les arcs sont représentés par des flèches dans le cas des graphes orientés
- les arêtes sont représentées par des segments dans le cas des graphes non orientés, c'est le cas de notre exemple.
- On appelle taille ou ordre du graphe le nombre de sommets du graphe.
Remarques.
- On se limitera dans ce chapitre à des graphes dans lesquels il y a au plus un arc entre deux sommets. On parle de 1-graphe.
- Les graphes sont une structure de donnée relationnelle : ils permettent de représenter des situations dans lesquelles des éléments sont en relations les uns avec les autres : internet, web, réseau social, réseau routier, carte, labyrinthe...
2 - Représentation d'un graphe orienté
Outre la représentation sagittale, il existe plusieurs moyens de représenter un graphe :
2.1 Tableau des successeurs
Définitions
S'il existe un arc (i; j) dans un graphe orienté, on dit que j est un successeur de i dans ce graphe.
Remarque.
On peut représenter un graphe par un tableau listant les successeurs de chaque sommet.
Exemple.
| Sommet | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Successeurs |
2.2 Tableau des prédécesseurs
Définitions
S'il existe un arc (i; j) dans un graphe orienté, on dit que j est un prédécesseur de i dans ce graphe.
Remarque.
On peut représenter un graphe par un tableau listant les prédécesseurs de chaque sommet.
Exemple.
| Sommet | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Prédécesseurs |
2.3 Matrice d'adjacence
Définitions
Exemple :
1 2 3 4 5
3 - Représentation d'un graphe non orienté
3.1 Tableau des voisins
Définitions
S'il existe un arc (i; j) dans un graphe non orienté, on dit que i et j sont voisins.
Remarque.
La notion de voisin est l'équivalent pour les graphes non orientés des notions de prédécesseur et de successeur. On peut représenter un graphe par un tableau listant les voisins de chaque sommet.
Exemple.
| Sommet | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Voisins |
3.3 Matrice d'adjacence
Exemple :
cliquez sur la matrice pour la modifier
4 - Exercices
4.1 Exercice 1
On considère notre réseau routier :
Etablir le tableau des villes voisines
| Ville | Epinal | Mulhouse | Nancy | Strasbourg | Vesoul |
|---|---|---|---|---|---|
| Voisins |
Donner la matrice d'ajacence du graphe
4.2 Exercice 2
On considère notre réseau routier mais avec certaines routes en sens unique :
Etablir le tableau des villes voisines
| Ville | Epinal | Mulhouse | Nancy | Strasbourg | Vesoul |
|---|---|---|---|---|---|
| Voisins |
Donner la matrice d'ajacence du graphe
4.3 Exercice 3
On considère le graphe orienté donné par les tableau des successeurs ci-dessous :
| Sommet | A | B | C | D | E |
|---|---|---|---|---|---|
| Successeurs | B | A, C, D | B | A |
Donner la matrice d'adjacence de ce graphe.
Tracer une représentation sagittale de ce graphe. https://app.diagrams.net/
4.4 Exercice 4
0n considère la matrice ci-dessous :
Cette matrice peut-elle correspondre à un graphe non orienté ?
Tracer une représentation sagittale du graphe associé à cette matrice (on appellera A, B et C ses sommets).
4.5 Exercice 5 : programmation
Le but de cet exercice est de construire des représentations de graphes en Python. Dans cet exercice les sommets seront représentés par des entiers de 0 à n-1 où n est 'ordre du graphe. Pour faciliter les tests, une fonction d'affichage est fournie dans le affichier à compléter.
- Copier et coller le code dans Thonny ou Edupython
- Dans Edupython :
- dans le menu outils - outils - installer un module avec conda, entrer
networkxet valider. - Dans Thonny :
- dans le menu outils - Gérer les Paquets...
- recherchez le module
networkxet installer-le. - Installer le module
networkx. - Intaller ensuite le module
matplotlibde la même manière.
Ce fichier contient :
- une fonction
afficher_grapheO, qui permet d'afficher des graphes orientés, et plus précisément les objets des classesGrapheOci-dessous, à conditions que toutes les méthodes aient été écrites, - une fonction afficher_grapheNO, qui permet d'afficher les objets de la classe
GrapheNOci-dessous, à conditions que toutes les méthodes aient été écrites.
1) Compléter le fichier avec une classe GrapheO permettant de représenter des graphes orientés
grâce à leur matrice d'adjacence et décrite ci-dessous :
- Attributs :
mat_adjde typelist[list[int]] - Méthodes :
-
__init__(self, n) -> void: initialise une matrice d'ajacence d'un graphe d'ordrensans aucun arc -
ordre(self) -> int: retourne l'ordre du graphe -
ajouter_arc(self,i,j) -> void: ajoute un arc du sommetiau sommetj -
existe_arc(self, i, j) -> bool: retourneTruesi il existe un arc du sommetiau sommetj -
liste_successeurs(self, i) -> list[int]: retourne la liste des successeurs du sommeti
-
2) Compléter le fichier avec une classe GrapheNO permettant de représenter des graphes non orientés grâce à leur matrice d'adjacence et décrite ci-dessous :
- Attributs :
mat_adj de type list[list[int]] - Méthodes :
__init__(self, n) -> void: initialise une matrice d'ajacence d'un graphe d'ordrensans aucun arcordre(self) -> int: retourne l'ordre du grapheajouter_arete(self,i,j) -> void: ajoute une arête entre les sommetsietjexiste_arete(self, i, j) -> bool: retourne True si il existe une arête entre les sommetsietjliste_voisins(self, i) -> list[int]: retourne la liste des voisins du sommeti
File des successeurs
A partir de notre graphe des villes on peut constituer la file des successeurs FS :
Commençons par Mulhouse comme sommet en se référant à la matrice d'adjacence, Mulhouse a pour successeurs Strasbourg, Vesoul, Epinal et Nancy et c'est tout (-).
On enfile les autres lignes de ma matrice d'adjacence et obtient la file FS suivante :

Il est conseillé de construire une liste APS contenant les Adresses des Premiers Successeurs.
5 - Parcours des graphes
5.1 Parcours en largeur
Chemin
Définitions
Exemple :
Distance
Définition
La distance entre deux sommets d'un graphe est la longueur du plus court chemin reliant ces deux sommets, si un tel chemin existe. Si un tel chemin n'existe pas, la distance entre les deux sommets n'est pas définie.
Exemple :
Parcours en largeur
Définitions
On considère un graphe, dans lequel on se fixe un sommet de départ. Dans le parcours en largeur du graphe, on visite :
Remarque.
Le parcours en largeur permet entre autres de déterminer les chemins les plus courts entre deux sommets. Il permet de ce fait de calculer la distance entre deux sommets.
Exemple :
Remarque.
Pour éviter de passer deux fois par le même sommet, il est nécessaire, lorsqu'on parcourt un graphe, de garder une trace des sommets déjà visités.
Exemple
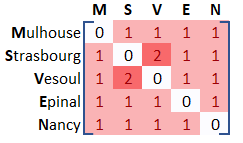
Cette fois, on construit la matrice qui permet de donner le nombre
d'arrêtes
minimales séparant deux sommets

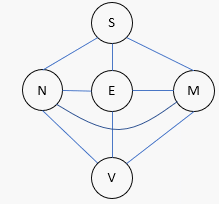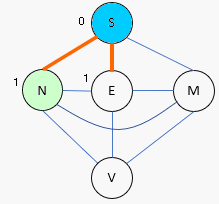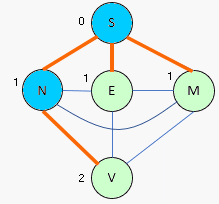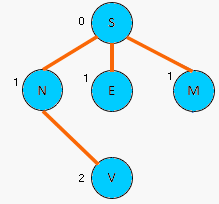
Partons de Strasbourg : On marque le sommet pour indiquer qu'il a
été visité puis on cherche les voisins. On marque les voisins et
progressivement on enlève les arrêtes des sommets déjà visités. Quand
tous les sommets sont marqués on obtient un arbre. Si On recommence en
partant d'un autre sommet (ville) on aura un arbre différent.
A partir d'un nœud source S, il liste d'abord les voisins de S pour ensuite les explorer un par un. Ce mode de fonctionnement utilise donc une file dans laquelle il prend le premier sommet et place en dernier ses voisins non encore explorés.
Les nœuds déjà visités sont marqués afin d'éviter qu'un même nœud soit exploré plusieurs fois. Dans le cas particulier d'un arbre, le marquage n'est pas nécessaire.
Étapes de l'algorithme :
1. Mettre le nœud source dans la file.
2. Retirer le nœud du début de la file pour le traiter.
3. Mettre tous les voisins non explorés dans la file (à la fin).
4. Si la file n'est pas vide reprendre à l'étape 2.
Note : l'utilisation d'une pile au lieu d'une file transforme l'algorithme du parcours en largeur en l'algorithme de parcours en profondeur.
5.2 Mise en pratique
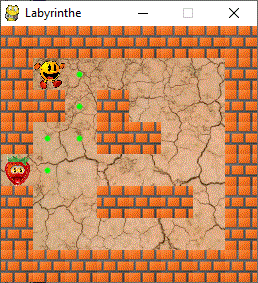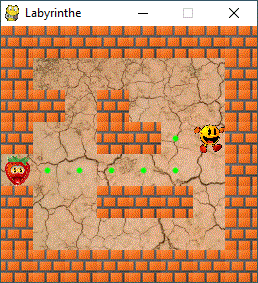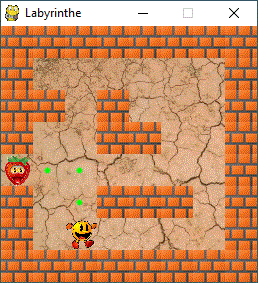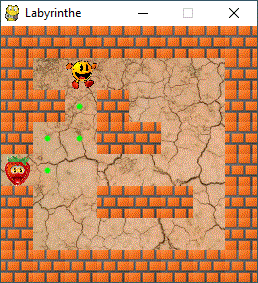
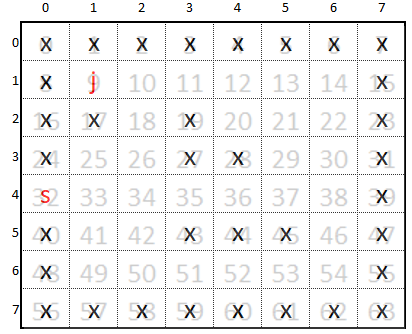
Le joueur (j) se trouve sur le sommet n°9 et la sortie (s) est au
n°32
Le graphe non orienté du labyrinthe est le suivant :
Matrice d'adjacence partielle du labyrinthe :
| 9
|
10 | 11 | 12 | 13 | 18 | 20 | 21 | 25 | 26 | 29 | 32 | 33 | 34 | 35 | 36 | 37 | |
| 9 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 13 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 18 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 21 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 26 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 29 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 32 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 34 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 37 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
5.2.1 - Création du graphe à partir des sommets
Télécharger puis décompresser le fichier Labyrinthe.zip. Ouvrir le fichier
Labyrinthe_EL.py et ajouter y les fonctions permettant de trouver le chemin le plus court vers la sortie, en appliquant la théorie les
graphes.
- Ecrire une fonction creer_graphe qui prend en paramètre
sommets : la liste des sommets,
- qui retourne 2-uplets : la matrice d'ajacence et l'objet de type GrapheNO
Algorithme :
Instancier un objet de classe GrapheNO ayant comme grandeur le nombre de sommets
Parourir les tous les sommets
si le sommet[i]+1 est dans la liste des sommets alors
ajouter une arrête entre sommets.index(sommets[i])et sommets.index(sommets[i]+1)
si le sommets[i]+larg_laby est dans la liste des sommets
ajouter une arrête entre sommets.index(sommets[i])et sommets.index(sommets[i]+larg_laby)
Retourner la matrice d'ajacence et l'objet GrapheNO
5.2.2 Programmation du parcours en largeur
Une façon de programmer un parcours en largeur est d'utiliser :
une liste deja_visites contenant tous les sommets déjà visités,
une file a_visiter contenant les prochains sommets à visiter,
une liste parcours,
Au début, deja_visites et parcours sont vides, a_visiter contient uniquement le sommet de départ.
Répèter jusqu'à ne plus avoir de sommet à visiter :
défiler un sommet (notons le s),
si s n'a pas déjà été visité :
ajouter s dans la liste deja_visites,
ajouter s dans la liste du parcours,
enfiler tous les voisins de s dans la file a_visiter.
retourner la liste du parcours largeur
- Écrire en Python la fonction
parcours_largeur qui prend en paramètre le graphe non orienté graphe et l'indice du sommet de la position du personnage depart,
- et retourne la liste des indices des sommets composant le parcours en largeur.
5.2.1 - Matrice d'adjacence :
Si on prend le sommet n° 26 : les sommets adjacents sont ceux qui sont :
- au-dessus : 26 - larg_laby
- en-dessous : 26 + larg_laby
- à gauche : 26 -1
- à droite : 26+1
Fonction matrice_adjacence
paramètres :
la liste des sommets
Résultat :
Liste contenant la matrice d'adjacence
DEBUT
matrice ← []
ligne ← []
Pour chaque sommet dans la liste des sommets
Pour chaque som dans la liste des sommets
si le sommet = som-1 ou sommet = som+1 ou sommet = som+larg_laby ou sommet = som-larg_laby
empiler 1 dans la liste ligne
sinon
empiler 0 dans la liste ligne
empiler la ligne à la matrice
ligne ← []
affiche_matrice(sommets,matrice) # appel de la fonction qui affiche la matrice pour vérifier le résultat
retourne matrice
Fin
2.3 - File des successeurs :

Il faut donc parcourir la matrice d'adjacence ligne par ligne et
rechercher les 1 qui correspondent aux sommets adjacents.
On ajoute ce sommet dans la liste
FS et on ajoute 0 pour terminer les successeurs. Au passage on
construit
la liste APS (l'Adresse des Premiers Successeurs).
Algorithme
Fonction File_successeurs
paramètres :
matrice : liste matrice d'adjacence
sommets : liste des sommets
Résultats :
FS : la liste contenant la file des successeurs
APS : la liste des adresses des premiers successeurs
DEBUT
FS ← []
APS ← []
pour i variant de 0 à la hauteur de la matrice
empiler la longueur de FS dans la liste APS
pour j variant de 0 à la largeur de la matrice
si matrice[i][j]=1
empiler sommets[j] à la liste FS
empiler 0 à la liste FS
empiler la longueur de FS dans la liste APS
retourne la liste des successeurs et les adresses des 1er successeurs
Fin
2.4- Parcours en largeur
On désire stocker la liste des sommets selon leur distance par
rapport au nœud :


Ex : pour le nœud 10, on souhaite générer une liste de l'arbre
suivant : [[10],[9,18,11],[12,26],[13,20,25,34],[14,...],...]
Algorithme
Fonction parcours_largeur
paramètres :
noeud : représente la case du joueur
Résultat:
arbre : liste contenant les distances du noeud à chaque sommet
Debut:
arbre ← [[noeud]]
file ← [0,noeud]
visites ← [] # liste des sommets déjà visités
Tant que la longueur de la file contient plus d'un élément
rang ← [] # liste qui permet de stocker les successeurs du sommet courant
Tant que le premier élément de la file est >0: # la valeur 0 permet d'indiquer la fin de la file courante
sommet ← défiler la file # sommet = file.pop()
Empiler le sommet à la liste visites
indice ← sommets.index(sommet) # recherche de la position du sommet courant dans la liste des sommets
pour i variant de APS[indice] à APS[indice+1]-1: # recherche des voisins du sommet dans FS en excluant 0
si FS[i] n'est pas dans la liste visites
Enfiler FS[i] dans rang # rang.insert(0,FS[i])
Enfiler FS[i] dans file
Empiler FS[i] dans visite
Défiler la file (qui doit être 0) # condition d'arrêt du tant que
Empiler à l'arbre la liste rang
Enfiler la valeur 0 dans la file
retourne la liste arbre
Fin
5.2.3 Recherche du chemin le plus court vers la sortie
Principe : on part de la sortie pour revenir vers la position joueur
Exemple de la sortie au sommet 32 :

Tant que la sortie n'a pas atteint la position du joueur :
On commence par réduire la liste du parcours largeur jusqu'au sommet 32,
On recherche la liste voisins de 32 qui est [33]
on parcours la liste des voisin et s'il se trouve être le sommet précédent on l'ajoute denas la liste du parcours : 33
Le sommet précédent devient la nouvelle sortie et le cycle recommence.
Cas du sommet 33 :
La liste du parcours lageur est réduite à [9,10,11,18,12,26,13,20,25,34,14,21]
Les voisins de 33 sont [25,32,34,41]
On a dans cette situation deux voisins qui sont également dans la liste du parcours : 25 et 34. Peut importe du voisin qu'on choisisa, puisque la longueur du chemin sera identique.
Chercher la colonne de la sortie dans la matrice d'ajacence et
trouver le prédécesseur dans la ligne correspondante.
Exemple le prédécesseur de 32 est 33 :
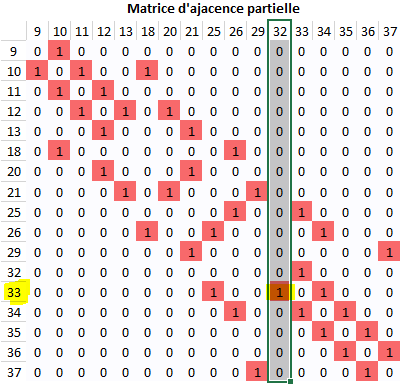
Algorithme :
ch est une liste vide et contiendra les indices des sommets
Tant que la sortie est différente de position alors
Réduire la liste parcours à l'indexe de la sortie
mémoriser dans une variables la liste des voisins de la sortie
Parcourrir la liste des voisins
si un voisin se trouve dans la liste des voisins
memoriser ce voisin
ajouter ce voisin au Chemin
remplacer la sortie par le voisin
retourner la liste des indexe des sommets
Ecrire en Python la fonction chemin qui prend en paramètres le graphe, le parcours largeur : la liste des indexes, sortie : l'indice de la sortie dans les sommets, pos : l'indice de la position du joueur dans la liste des sommets.
Colez votre code python ci-dessous :
Télécharger puis décompresser le fichier Labyrinthe.zip. Ouvrir le fichier Labyrinthe_EL.py et ajouter y les fonctions permettant de trouver le chemin le plus court vers la sortie, en appliquant la théorie les graphes.
- Ecrire une fonction creer_graphe qui prend en paramètre
sommets: la liste des sommets, - qui retourne 2-uplets : la matrice d'ajacence et l'objet de type GrapheNO
Algorithme :
Instancier un objet de classe GrapheNO ayant comme grandeur le nombre de sommets Parourir les tous les sommets si le sommet[i]+1 est dans la liste des sommets alors ajouter une arrête entre sommets.index(sommets[i])et sommets.index(sommets[i]+1) si le sommets[i]+larg_laby est dans la liste des sommets ajouter une arrête entre sommets.index(sommets[i])et sommets.index(sommets[i]+larg_laby) Retourner la matrice d'ajacence et l'objet GrapheNO
Une façon de programmer un parcours en largeur est d'utiliser :
une liste deja_visites contenant tous les sommets déjà visités, une file a_visiter contenant les prochains sommets à visiter, une liste parcours, Au début, deja_visites et parcours sont vides, a_visiter contient uniquement le sommet de départ. Répèter jusqu'à ne plus avoir de sommet à visiter : défiler un sommet (notons le s), si s n'a pas déjà été visité : ajouter s dans la liste deja_visites, ajouter s dans la liste du parcours, enfiler tous les voisins de s dans la file a_visiter. retourner la liste du parcours largeur
- Écrire en Python la fonction
parcours_largeurqui prend en paramètre le graphe non orientégrapheet l'indice du sommet de la position du personnagedepart, - et retourne la liste des indices des sommets composant le parcours en largeur.
5.2.1 - Matrice d'adjacence :
Si on prend le sommet n° 26 : les sommets adjacents sont ceux qui sont :- au-dessus : 26 - larg_laby
- en-dessous : 26 + larg_laby
- à gauche : 26 -1
- à droite : 26+1
Fonction matrice_adjacence
paramètres :
la liste des sommets
Résultat :
Liste contenant la matrice d'adjacence
DEBUT
matrice ← []
ligne ← []
Pour chaque sommet dans la liste des sommets
Pour chaque som dans la liste des sommets
si le sommet = som-1 ou sommet = som+1 ou sommet = som+larg_laby ou sommet = som-larg_laby
empiler 1 dans la liste ligne
sinon
empiler 0 dans la liste ligne
empiler la ligne à la matrice
ligne ← []
affiche_matrice(sommets,matrice) # appel de la fonction qui affiche la matrice pour vérifier le résultat
retourne matrice
Fin
2.3 - File des successeurs :

Il faut donc parcourir la matrice d'adjacence ligne par ligne et rechercher les 1 qui correspondent aux sommets adjacents.
On ajoute ce sommet dans la liste FS et on ajoute 0 pour terminer les successeurs. Au passage on construit la liste APS (l'Adresse des Premiers Successeurs).
Algorithme
Fonction File_successeurs
paramètres :
matrice : liste matrice d'adjacence
sommets : liste des sommets
Résultats :
FS : la liste contenant la file des successeurs
APS : la liste des adresses des premiers successeurs
DEBUT
FS ← []
APS ← []
pour i variant de 0 à la hauteur de la matrice
empiler la longueur de FS dans la liste APS
pour j variant de 0 à la largeur de la matrice
si matrice[i][j]=1
empiler sommets[j] à la liste FS
empiler 0 à la liste FS
empiler la longueur de FS dans la liste APS
retourne la liste des successeurs et les adresses des 1er successeurs
Fin
2.4- Parcours en largeur
On désire stocker la liste des sommets selon leur distance par rapport au nœud :


Ex : pour le nœud 10, on souhaite générer une liste de l'arbre
suivant : [[10],[9,18,11],[12,26],[13,20,25,34],[14,...],...]
Fonction parcours_largeur
paramètres :
noeud : représente la case du joueur
Résultat:
arbre : liste contenant les distances du noeud à chaque sommet
Debut:
arbre ← [[noeud]]
file ← [0,noeud]
visites ← [] # liste des sommets déjà visités
Tant que la longueur de la file contient plus d'un élément
rang ← [] # liste qui permet de stocker les successeurs du sommet courant
Tant que le premier élément de la file est >0: # la valeur 0 permet d'indiquer la fin de la file courante
sommet ← défiler la file # sommet = file.pop()
Empiler le sommet à la liste visites
indice ← sommets.index(sommet) # recherche de la position du sommet courant dans la liste des sommets
pour i variant de APS[indice] à APS[indice+1]-1: # recherche des voisins du sommet dans FS en excluant 0
si FS[i] n'est pas dans la liste visites
Enfiler FS[i] dans rang # rang.insert(0,FS[i])
Enfiler FS[i] dans file
Empiler FS[i] dans visite
Défiler la file (qui doit être 0) # condition d'arrêt du tant que
Empiler à l'arbre la liste rang
Enfiler la valeur 0 dans la file
retourne la liste arbre
Fin
Principe : on part de la sortie pour revenir vers la position joueur
Exemple de la sortie au sommet 32 :
Tant que la sortie n'a pas atteint la position du joueur :
Le sommet précédent devient la nouvelle sortie et le cycle recommence.
Cas du sommet 33 :
La liste du parcours lageur est réduite à [9,10,11,18,12,26,13,20,25,34,14,21]
Les voisins de 33 sont [25,32,34,41]
On a dans cette situation deux voisins qui sont également dans la liste du parcours : 25 et 34. Peut importe du voisin qu'on choisisa, puisque la longueur du chemin sera identique.
Chercher la colonne de la sortie dans la matrice d'ajacence et trouver le prédécesseur dans la ligne correspondante.
Exemple le prédécesseur de 32 est 33 :

Algorithme :
ch est une liste vide et contiendra les indices des sommets Tant que la sortie est différente de position alors Réduire la liste parcours à l'indexe de la sortie mémoriser dans une variables la liste des voisins de la sortie Parcourrir la liste des voisins si un voisin se trouve dans la liste des voisins memoriser ce voisin ajouter ce voisin au Chemin remplacer la sortie par le voisin retourner la liste des indexe des sommets
Ecrire en Python la fonction chemin qui prend en paramètres le graphe, le parcours largeur : la liste des indexes, sortie : l'indice de la sortie dans les sommets, pos : l'indice de la position du joueur dans la liste des sommets.
Colez votre code python ci-dessous :
5.3 Algorithme de recherche de chemin
Les algorithmes de recherche de chemin, travaillent sur des graphes pondérés (par exemple pour rechercher la route entre un point de départ et un point d'arrivée dans un logiciel de cartographie). Ces algorithmes recherchent aussi souvent les chemins les plus courts. On peut citer l'algorithme de Dijkstra ou encore l'algorithme de Bellman-Ford qui recherchent le chemin le plus court entre un noeud de départ et un noeud d'arrivée dans un graphe pondéré.
La vidéo ci-dessous explique le principe de fonctionnement de l'algorithme de Dijkstra.
La vidéo ci-dessous explique le principe de fonctionnement de l'algorithme de Prim.
Fond : Texte : Tables : Thème du langage:
Contenu
sous licence CC BY-NC-SA 3.0
Pascal Hassenforder - Amandine Schreck 13/10/2020
MAJ le 16/04/2024