NUMERIQUE ET SCIENCES INFORMATIQUES

Niveau : Terminale générale, enseignement de spécialité NSI

D
É
C
O
N
N
E
C
T
É

Programmation dynamique

1. Principe

Définition

La programmation dynamique est un principe algorithmique permettant d'améliorer la complexité temporelle de la résolution d'un problème dans certaines situations.

Cette définition est un peu vague et nous en verrons une plus précise par la suite. Nous retrouverons dans cette partie des notions de récursivité et même des similitudes avec le principe de diviser pour régner.

Nous allons donc tenter de ...

  • distinguer la programmation dynamique de ces différentes situations,
  • définir les principes de la programmation dynamique
  • mettre en applications les principes de la programmation dynamique dans différentes situations.

Mais nous allons commencer par un exemple que vous avez déjà vu en récursivité.

2. Suite de fibonacci

La suite de Fibonacci a été inventée au Moyen-Age dans le but de tenter de modéliser l'évolution d'une population de lapins ( plus de détails ici par exemple )

Elle est définie ainsi :

  • pour n = 0 : F0 = 0
  • pour n = 1 : F1 = 1
  • pour n >=2 : Fn = Fn-1 + Fn-2

→ en dehors des deux premiers cas, chaque terme de la suite de Fibonacci est donc égal à la somme des deux termes précédents :

n Fn
0 0
1 1
2 0 + 1 = 1
3 1 + 1 = 2
4 1 + 2 = 3
5 2 + 3 = 5
6 3 + 5 = 8
... ...

Vous avez déjà programmé cette suite grâce à une fonction récursive que vous pouvez voir ci-dessous :

		
		
			
			
Cette écriture est très simple, et très lisible : on retrouve bien à la ligne 13 la définition de la suite de Fibonacci pour n >=2
			
Cependant, la complexité en temps de cette fonction est très mauvaise, elle est de l'ordre de 2n (exactement 1,6n), c'est à dire exponentielle.

			Ne cherchez même pas à calculer le terme de rang n = 1000, le temps est déjà très long pour n = 50 !

			Nous allons donc tenter d'optimiser cette fonction grâce au principe de la programmation dynamique.
			Pour cela nous allons analyser les appels récursifs réalisés lors de l'appel de fib(6).
			

			

				

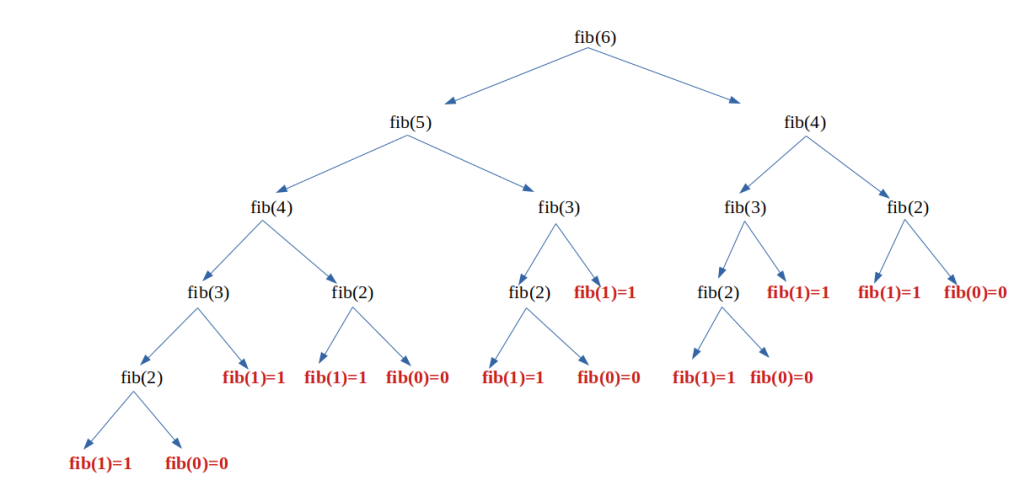
					appels récursifs fibonacci					
				
			
			

			

			Une fois que tout ces appels sont réalisés, il faut bien sur les additionner en "remontant l'arbre"...Vous pouvez imaginer la complexité du processus pour fib(30) !

			On peut remarquer qu'ici, si la récursivité présente un code particulièrement lisible, mais ce code n'est pas efficace du tout !


			Si l'on regarde de plus près l'arbre précédent, on peut constater que l'on fait plusieurs fois la même chose :
			

				

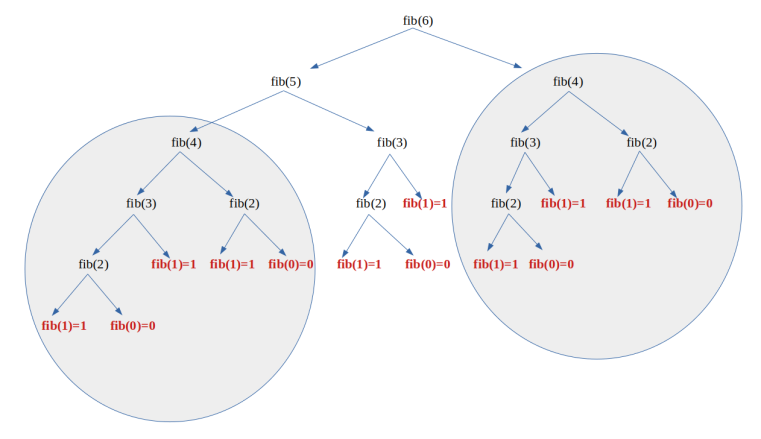
					appels récursifs fibonacci					
				
			
			
		
			
	
			On calcule par exemple deux fois le terme fib(4) et même si l'on analyse encore plus ...
			

			

			

				

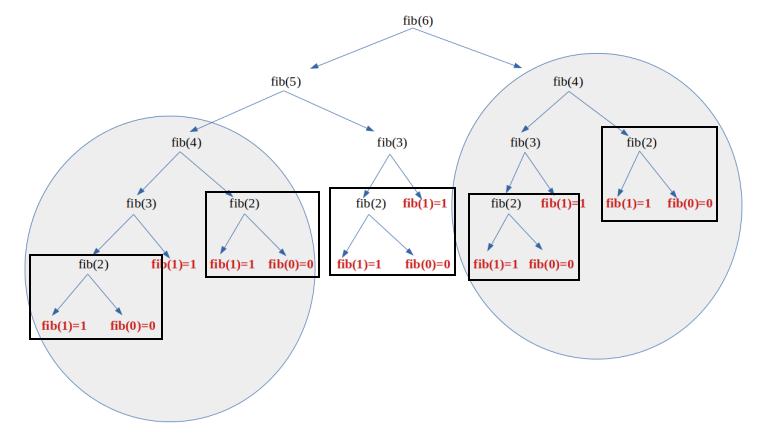
					appels récursifs fibonacci					
				
			
			
	
				
			
On peut remarquer que l'on calcule 3 fois fib(3) et 5 fois fib(2)...

			Il va falloir optimiser tout cela grâce à la programmation dynamique.
 
		
			
Nous allons travailler par mémoïsation (non ce n'est pas une faute de frappe !), c'est à dire que l'on va conserver les résultats intermédiaires dans un tableau afin de remplacer un nouveau calcul par un appel mémoire, beaucoup plus économe en temps.

			
La  mémoïsation fait partie de la programmation dynamique.

			
			
			
			
					
		
			

			
				
			

			Nous pouvons constater que dans ce code :
			
    
				
  • La structure est assez proche de celle de la version récursive
    • 
				
  • Les résultats sont stockés dans un tableau.
    • 
				
  • Le calcul nécessite de travailler sur deux fonctions (la création du tableau de mémoïsation ne peut pas se faire à l'intérieur de la fonction récursive).
    • 
				
  • Avant d’effectuer les appels récursifs on vérifie que le terme n’a pas déjà été calculé. Chaque valeur n’est donc calculée qu’une seule fois.
    • 
			

			

				
Le code précédent propose une approche mettant en œuvre la récursivité et la mémoïsation, c'est une des deux approches de la programmation dynamique. Elle est appelée aussi "du haut vers le bas" ou encore "top-down" car elle part du haut de l'arbre des appels récursifs vu précédemment.
			
			
			


			

				
Les deux codes de calcul de la suite de Fibonacci ne sont pas si différents finalement. Nous allons tenter de tester leur efficacité.

				
    
					
  1. Tester la durée de calcul du 30ème terme de la suite de Fibonacci avec les deux fonctions ci-dessus et notez vos constatations.
    2. 
					
						
    
					
					
  2. Quel est l'avantage de la programmation dynamique ?
    3. 
					
    
					
					
  3. Quel est l'inconvénient de la mémoïsation ?
    4. 
					
    
					
				
	
			
	
			
		
			
		
			
Il existe aussi une autre approche possible en programmation dynamique, "du bas vers le haut" ou encore "bottom-up". Cette approche consiste à parcourir l'arbre ds appels récursifs en partant du bas.

			
On remarque alors que dans ce cas, il n'est plus nécessaire de faire appel à la récursivité.

			
Le code correspondant pour calculer la suite de Fibonacci serait : 

			
			
			
			
					
		
			

			
		

			
				
			

			
On peut également remarquer que :

			
    
				
  • la dénomination "de bas en haut" est justifiée, on part bien du bas de l'arbre et on le remonte jusqu'à la racine. 

    • 
				
  • le code ressemble beaucoup à ce que l'on à fait "à la main" dans le tableau de présentation de la suite de Fibonacci.

    • 
				
  • Dans le cas de la suite de Fibonacci, la programmation dynamique du bas vers le haut est en fait la solution "naïve" de résolution du problème.

    • 
				
  • Comme dans la solution "du haut vers le bas", les résultats intermédiaires sont stockés dans un tableau.
    • 
			

			
				

			

		

2. Les principes fondamentaux de la programmation dynamique



	
2.1. Dans quelle situations utilises-t-on la programmation dynamique ?

	

		
    
			
  • La programmation dynamique résout un problème, comme "diviser pour régner", en combinant les solutions de sous problèmes similaires mais plus petits. 
    • 
			
  • Contrairement à "diviser pour régner" les sous problèmes ne sont pas complémentaires (par exemple la recherche dans le tableau gauche ou le tableau droit lors d'une recherche par dichotomie)
    • 
			
  • Dans la programmation dynamique, les sous problèmes se chevauchent (comme les différents appels récursif lors du calcul de la suite de Fibonacci)
    • 
			
  • Les sous problèmes se "chevauchant", il est possible 
			
      
				
    • Soit de stocker les résultats intermédiaires pour éviter de les calculer plusieurs fois. C'est la mémoïsation
      • 
				
    • Soit aborder le problème "de bas en haut" (en partant du bas de l'arbre représentant le problème) avec la possibilité là aussi de stocker les résultats intermédiaires. 
      • 
			
    
			
  • Le mot "programmation" dans "programmation dynamique", ne fait par référence à l'utilisation d'un langage de programmation, mais plutôt comme synonyme de planification et ordonnancement 
    • 			
		

		
Contrairement à la récursivité, il n'est pas aisé de reconnaître la programmation dynamique dans un programme ou un algorithme.

		
Cependant à chaque fois que l'on utilise la récursivité il est important de se demander si une optimisation mettant en œuvre la programmation dynamique n'est pas envisageable. 

	

	
2.2. Comment construire un code en programmation dynamique ?

	

		
Pour concevoir une fonction en programmation dynamique, il faut le plus souvent:

					
    
						
  • Repérer les sous problèmes.
    • 
						
  • Identifier une relation de récurrence entre les sous problèmes.
    • 		
						
  • Repérer les chevauchements possibles (par exemple en construisant un arbre d'appels liés à la relation de récurrence).
    • 
						
  • En déduire l'algorithme correspondant :
						
      
							
    • Soit grâce à la récursivité et la mémoïsation (programmation dynamique de haut en bas) 
      • 
							
    • Soit grâce au stockage des résultats successifs dans un tableau (programmation dynamique de bas en haut) 
      • 
							
						
    										
						
    • 
					

	




4. Programmation dynamique et rendu de monnaie 



	
Nous allons maintenant travailler sur un problème d'optimisation déjà rencontré l'année dernière : le problème du rendu de monnaie.
		

		

			Petit rappel : vous avez à votre disposition un nombre illimité de pièces de 2 cts, 5 cts, 10 cts, 50 cts et 1 euro (100 cts). Vous devez rendre une certaine somme (rendu de monnaie). Le problème est le suivant : "Quel est le nombre minimum de pièces qui doivent être utilisées pour rendre la monnaie"
		

		

			La résolution "gloutonne" de ce problème peut être la suivante :
		

		
    
			
  1. 
				on prend la pièce qui a la plus grande valeur (il faut que la valeur de cette pièce soit inférieure ou égale à la somme restant à rendre)
			
    2. 
			
  2. 
				on recommence l'opération ci-dessus jusqu'au moment où la somme à rendre est égale à zéro.
			
    3. 
		

		

			Prenons un exemple :
		

		

			nous avons 1 euro 77 cts à rendre :
		

		
    
			
  • 
				on utilise une pièce de 1 euro (plus grande valeur de pièce inférieure à 1,77 euro), il reste 77 cts à rendre
			
    • 
			
  • 
				on utilise une pièce de 50 cts (plus grande valeur de pièce inférieure à 0,77 euro), il reste 27 cts à rendre
			
    • 
			
  • 
				on utilise une pièce de 10 cts (plus grande valeur de pièce inférieure à 0,27 euro), il reste 17 cts à rendre
			
    • 
			
  • 
				on utilise une pièce de 10 cts (plus grande valeur de pièce inférieure à 0,17 euro), il reste 7 cts à rendre
			
    • 
			
  • 
				on utilise une pièce de 5 cts (plus grande valeur de pièce inférieure à 0,07 euro), il reste 2 cts à rendre
			
    • 
			
  • 
				on utilise une pièce de 2 cts (plus grande valeur de pièce inférieure à 0,02 euro), il reste 0 cts à rendre
    • 
		

		

			L'algorithme se termine en renvoyant 6 (on a dû rendre 6 pièces)
		

		
		
Voici la fonction récursive du rendu de momnaie glouton :

		
			
			
					
		
			

			
		
		
		
rendu_monnaie_rec(pieces,177) demande beaucoup trop d'appel récursif et plante le programme.

		
Comme vous avez peut-être déjà dû le remarquer, même dans le cas simple évoqué ci-dessus (11 cts à rendre), nous faisons plusieurs fois exactement le même calcul. Par exemple on retrouve 2 fois la branche qui part de "4" : 

		
		
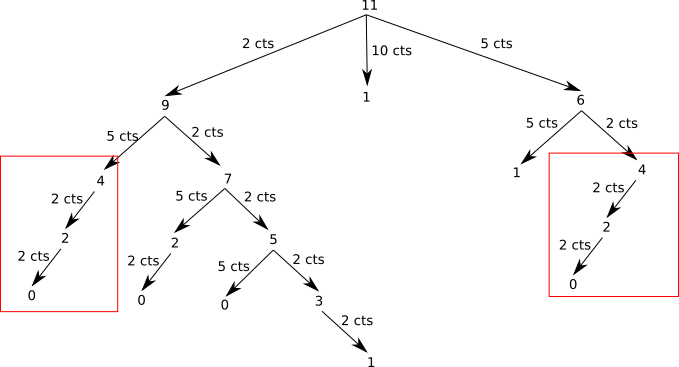
Il va donc être possible d'appliquer la même méthode que pour Fibonacci : la programmation dynamique.


		
À noter que dans des cas plus "difficiles à traiter" comme 1,71 euro, on va retrouver de nombreuses fois exactement les mêmes calculs, il est donc potentiellement intéressant d'utiliser la programmation dynamique. 

		
		
Compléter la version dynamique de la fonction rendu_monnaie_rec ci-dessous :



			
		
			
			
					
		
			

			
	
			
			
		
			
			
			




5. Exercice : Optimisation de la découpe de planches
		
			planche en bois	
			
Présentation du problème

			

						
				
Nous allons considérer qu'une scierie reçoit des planches de longueur l entière.

				La scierie découpe ces planches en morceaux de longueur également entière et les revend selon selon une grille tarifaire donnée :

				

				
				

				longueur (m)
				0        
				1
				2
				3
				4
				5
				6
				7
				8
				9
				10
				

				

				prix (€)
				0        
				1
				5
				8
				9
				10
				15
				17
				20
				24
				30
				

				
				


				
							

							
			
L'objectif est donc de découper chaque planche de façon optimale pour en tirer un prix maximum.	
	
			
		
			
Résolutions du problème

			
			
			
Afin de bien appréhender le problème répondez aux questions ci dessous :

			
    
				
  1. Présenter Toutes les découpes possibles pour une planche de longueur 4 sous forme d'un arbre.
    2. 
				
  2. Déterminer le revenu de chaque découpe possible
    3. 
				
  3. En déduire la découpe optimale pour une planche de longueur 4
    4. 
				
				
    
	
			
		
		
				
			

			
		
5.1. Solution récursive

		

		
Nous allons tenter de coder une fonction coupe_recurs ayant pour argument la longueur n de la planche et le tableau p des prix et qui renverra la revenu optimal que l'on peut tirer de la planche.

		
				
		
    
				
  1. Si l'on décide de faire une première découpe de longueur i dans la planche, quelle sera la longueur de la planche restante
    2. 
				
    
				
  2. Si l'on décide de faire une première découpe de longueur i dans la planche, quel sera le revenu optimal en fonction de p[i] et de coupe_recurs(n-i,p) ?
    3. 
				
    

				
  3. Déduire des questions précédentes un algorithme récursif résolvant le problème, et coder cet algorithme.
    4. 			
			

			
		
		

		
	

			
			
			
			
					
		
			

			
	

			
		
			
			
			
		

		
5.2 Solutions dynamiques

		
5.2.1 Du haut vers le bas

		

		
Comme d'habitude, la solution récursive est simple à coder mais n'est pas très efficace....

		
Nous pouvons constater que nous sommes en présence d'un problème d'optimisation.

		
Nous allons maintenant chercher les sous problèmes et leurs chevauchements.

				
		
    
				
  1. Dans l'arbre précédent, entourer les deux plus grands sous arbres identiques
    2. 

				
  2. Quelle est la taille de cet arbre ?
    3. 
				
    
				
  3. De façon générale, si la planche a pour longueur n, quelle sera la taille de cet arbre ?
    4. 
				
    
		

		
			
		
					
		
			
	
		
		
			
			
					
		
			

			
	
			
		
					
				

		

	
		

		
5.2.2 Du bas vers le haut

		

			
		
		
			
			
					
		
			

			
	
			
		
					
		
		

		
	
		
		
		
		
	



    

    

	    










































































Fond :   
 Texte :    
 Tables :   
 Thème du langage: