 SCIENCES NUMERIQUES ET TECHNOLOGIE
SCIENCES NUMERIQUES ET TECHNOLOGIE
Niveau : Seconde SNT
 SCIENCES NUMERIQUES ET TECHNOLOGIE
SCIENCES NUMERIQUES ET TECHNOLOGIENiveau : Seconde SNT
La Géolocalisation |
Le Global Positioning System (GPS) ou « Géo-positionnement par satellite », est un système de positionnement par satellites appartenant au gouvernement des États-Unis. Mis en place par le département de la Défense des États-Unis à des fins militaires, le système avec 24 satellites est totalement opérationnel en 1995 et s’ouvre au civil en 2000.
Les 24 satellites de constellation GPS sont situés à 20184 km d’altitude, et font le tour de la terre en 12h
Répondre aux questions suivantes :
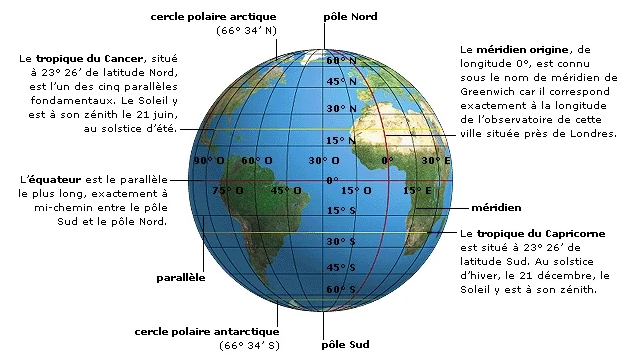
Lancer un navigateur puis aller sur le site https://www.coordonnees-gps.fr/
Déterminer alors les coordonnées GPS du lycée Lavoisier
| Latitude (décimal) | |
|---|---|
| Latitude (DMS) | |
| Longitude (décimal) | |
| Longitude (DMS) | |
| Altitude |
Localement, sur une petite surface, on peut assimiler la sphère terrestre à un plan.
On peut considérer que la variation de la longitude ou de la latitude est proportionnelle à la variation de l’abscisse x ou de l’ordonnée y.
Autrement dit : longitude = f(x) et latitude = g(y) avec f et g deux fonctions affines
À l’aide du site https://www.coordonnees-gps.fr remplir de tableau suivant :
| Ville | Mulhouse | Orléans | Marseille | Brest | Lille | Bordeaux |
|---|---|---|---|---|---|---|
| abscisse (écran) : x | ||||||
| ordonnée (écran) : y | ||||||
| longitude (à 10−4 près) : | ||||||
| latitude (à 10−4 près) : |
La fonction f permettant de passer de x à la longitude est une fonction affine définie par f (x) = ax + b
À l’aide des données recueillies pour les longitudes et abscisses de Mulhouse et Brest, écrire un système d’équations, d’inconnues a et b.
A l'aide de la calculatrice résoudre ce système d'équations à deux inconnues.
 , valider avec la touche "OK",
, valider avec la touche "OK",f(x) = *x+
Vérifier que le déplacement horizontal du curseur sur la carte correspond maintenant à la longitude.
À l’aide des données recueillies pour les latitudes et ordonnées de Marseille et Lille, écrire un système d’équations, d’inconnues a et b
Résoudre le système d'équations à l'aide de la calculatrice, puis reporter ci-dessous les coefficients de a et b qui forment la fonction f(x).
g(y) = *x+
Vérifier que le déplacement vertical du curseur sur la carte correspond maintenant à la latitude.
Le but de cette partie est d’apprendre à interpréter les données géographiques à partir d’un signal GPS reçu (appelé trame GPGGA) par un appareil situé au sol (smartphone, boitier situé dans une voiture,...)

Un récepteur GPS reçoit le type de signal suivant :
$GPGGA,064036.289,4836.5375,N,00740.9373,E,1,04,3.2,200.2,M„„*0E
Comment interpréter ce signal ?
| $GPGGA | Type de trame (ici trame GPS) |
|---|---|
| 064036.289 | Trame envoyée à 06h 40m 36,289s (heure UTC) |
| 4836.5375,N | Latitude : 48°36,5375’ = 48,608958° Nord |
| 00740.9373,E | Longitude : 7°40.9373’= 7,682288° Est |
| 1 | Type de positionnement (1 signifie positionnement GPS) |
| 04 | Nombre de satellites utilisés pour calculer les coordonnées |
| 3.2 | Précision horizontale ou HDOP (Horizontal dilution of precision) |
| 200.2,M | Altitude 200.2 mètres |
$GPGGA,113239.512,4545.47208,N,0449.93164,E,1,08,0.6,3.4,155.3,M„,4A"
Le but de cette partie est de récupérer la longitude et latitude d'une trame provenant d'un récepteur GPS.
Dans le programme ci-dessous, la fonction latitude permet de retourner la latitude au format décimal.
trame ="$GPGGA,123519.512,4745.6689,N,00719.8057,E,1,08,0.9,545.4,M,241.0,M,,*67"
liste = trame.split(",")
Désormais liste[0] contient $GPGGA, liste[1] contient 123519.512, liste[2] contient 4745.6689, etc.
print(latitude(liste))
latitude, puis modifier-la pour en faire une fonction qui retourne la longitude.print(longitude(liste))
Saurez-vous me dire où et quand la photo a été prise ?

Un des problèmes classiques en informatique est de trouver le plus court chemin reliant deux éléments d'un même réseau, que ce soit deux villes dans un réseau routier ou deux routeurs d'un réseau informatique.
On considère l'extrait de carte de la région Auvergne-Rhône-Alpes donné ci-dessous :
Un technicien d'une entreprise doit se déplacer et pouvoir intervenir sur les différents sites de cette entreprises, situés dans les villes suivantes : Aurillac (A), Bourg-en-Bresse (B), Clermont-Ferrand (C), Saint-Etienne (E), Grenoble(G), Lyon (L), Le Puy-en-Velay(P), Valence(V). Il connait les distances suivantes par autoroute, en km :
Donner une représentation graphique simplifiée de la situation présentée ci-dessus.
Connectez-vous afin de pouvoir téléverser vos fichiers en ligne
Edsger Dijkstra
Edsger Wybe Dijkstra (mathématicien et informaticien néerlandais 1930 − 2002) a proposé en 1959 un algorithme qui permet de calculer le plus court chemin entre un sommet particulier et tous les autres. C'est l'un des plus efficaces pour traiter les problèmes de plus court chemin. Grâce à la puissance du traitement informatique, il est utilisé par les logiciels d'optimisation de trajets réels (Navigateurs GPS, Site RATP. . .) ou virtuels (routage internet). Cet algorithme ne fonctionne que si le graphe ne possède que des valeurs positives.

Algorithme de Dijkstra
Pour faciliter la recherche du plus court chemin il est commode de présenter les résultats dans un tableau.
| Etape n° | Sommet choisi | A | B | C | E | G | L | P | V |
|---|---|---|---|---|---|---|---|---|---|
| 0 | Initialisation | ∞ | 0 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| 1 | ∞ | X | ∞ | ∞ | 180(B) | 80(B) | ∞ | ∞ | |
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 | |||||||||
| 6 | |||||||||
| 7 |
Vérifier vos résultats sur https://graphonline.ru/fr/ menu "Algorithme" - "Plus court chemin avec l'algorithme de Dijkstra". Sélectionner "rapport complet".
La route entre Le Puy-en-Velay et Aurillac est fermée à la circulation. Quel chemin doit-il alors emprunter ?
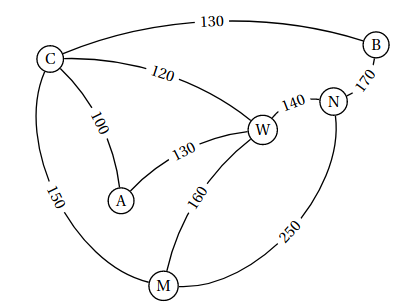
Alexis part en voyage dans l’Est des Etats-Unis. Il souhaite visiter les villes suivantes : Atlanta (A), Boston (B), Chicago (C), Miami (M), New York (N)et Washington (W). Une compagnie aérienne propose les liaisons suivantes représentées par le graphe ci-dessous :
| Etape n° | Sommet choisi | A | B | C | M | N | W |
|---|---|---|---|---|---|---|---|
| 0 | |||||||
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 |

| Partie 1 (12 pts) | Partie 2 (5 pts) | Partie 3 (0.5 pt) | Partie 4 (5.5 pts) | Total (23 pts) | Note (20 pts) |
|---|---|---|---|---|---|
| 0 | 0 |
auteurs : DENIS NOWAKOWSKI, Lycée Camille Corot
F.Vergniaud
MAJ par P. Hassenforder le 18/11/2024